Question
Question: $\lim_{x \to 2^+} \lceil x^2 - 5x + 6 \rceil$...
limx→2+⌈x2−5x+6⌉
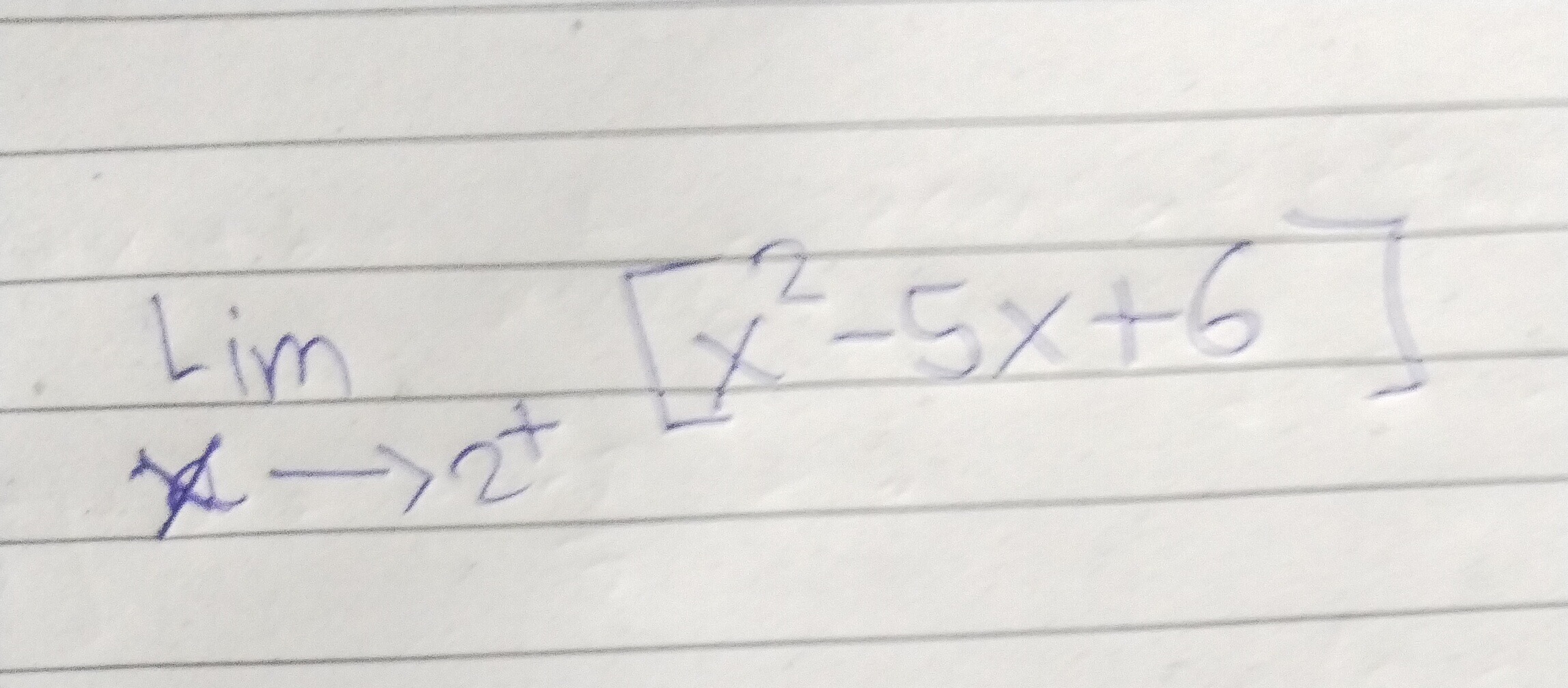
-1
0
1
2
0
Solution
To evaluate the limit limx→2+⌈x2−5x+6⌉, we first analyze the expression inside the ceiling function, let g(x)=x2−5x+6.
Step 1: Evaluate the inner function at the limit point. Substitute x=2 into g(x): g(2)=(2)2−5(2)+6=4−10+6=0.
Step 2: Determine the behavior of the inner function as x approaches 2 from the right side (x→2+). We need to know if g(x) approaches 0 from values greater than 0 (i.e., 0+) or from values less than 0 (i.e., 0−). The quadratic expression g(x)=x2−5x+6 can be factored as g(x)=(x−2)(x−3).
As x→2+:
- The term (x−2) will be a small positive number (e.g., if x=2.001, x−2=0.001). We denote this as 0+.
- The term (x−3) will approach 2−3=−1.
Therefore, g(x)=(x−2)(x−3) approaches (0+)(−1). The product of a small positive number and a negative number is a small negative number. So, g(x) approaches 0 from the negative side, which we denote as 0−.
Step 3: Evaluate the ceiling function with the determined behavior. Let y=g(x). As x→2+, y→0−. Now we need to find limy→0−⌈y⌉. The ceiling function ⌈y⌉ gives the smallest integer greater than or equal to y. If y is a number slightly less than 0 (for example, y=−0.001, y=−0.5, or y=−0.99), the smallest integer greater than or equal to y is 0. For instance: ⌈−0.001⌉=0 ⌈−0.5⌉=0 ⌈−0.99⌉=0
Thus, limy→0−⌈y⌉=0.
Combining these steps, we get: limx→2+⌈x2−5x+6⌉=limy→0−⌈y⌉=0.
