Solveeit Logo
Login

Question

Question: $\lim_{x \to 1} \frac{\sqrt[3]{7+x^3}-\sqrt{3+x^2}}{x-1}$ is equal to...

lim⁡x→17+x33−3+x2x−1\lim_{x \to 1} \frac{\sqrt[3]{7+x^3}-\sqrt{3+x^2}}{x-1} is equal to

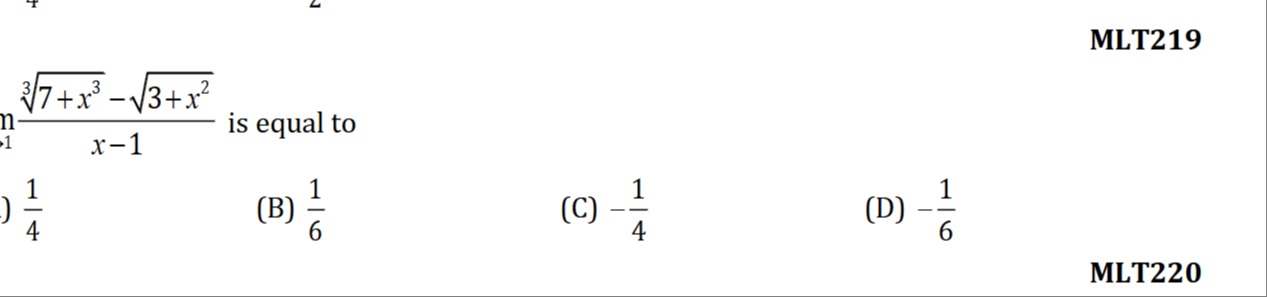
A

14\frac{1}{4}

B

16\frac{1}{6}

C

−14-\frac{1}{4}

D

−16-\frac{1}{6}

Answer

−14-\frac{1}{4}

Explanation

Solution

The limit is of the indeterminate form 00\frac{0}{0}. Applying L'Hopital's Rule, we differentiate the numerator and the denominator with respect to xx.

The derivative of the numerator is: ddx(7+x33−3+x2)=ddx((7+x3)1/3)−ddx((3+x2)1/2)\frac{d}{dx}(\sqrt[3]{7+x^3} - \sqrt{3+x^2}) = \frac{d}{dx}((7+x^3)^{1/3}) - \frac{d}{dx}((3+x^2)^{1/2}) =13(7+x3)−2/3(3x2)−12(3+x2)−1/2(2x)= \frac{1}{3}(7+x^3)^{-2/3}(3x^2) - \frac{1}{2}(3+x^2)^{-1/2}(2x) =x2(7+x3)−2/3−x(3+x2)−1/2= x^2(7+x^3)^{-2/3} - x(3+x^2)^{-1/2}

The derivative of the denominator is: ddx(x−1)=1\frac{d}{dx}(x-1) = 1

The limit becomes: lim⁡x→1x2(7+x3)−2/3−x(3+x2)−1/21\lim_{x \to 1} \frac{x^2(7+x^3)^{-2/3} - x(3+x^2)^{-1/2}}{1}

Substituting x=1x=1: (1)2(7+13)−2/3−(1)(3+12)−1/2(1)^2(7+1^3)^{-2/3} - (1)(3+1^2)^{-1/2} =(8)−2/3−(4)−1/2= (8)^{-2/3} - (4)^{-1/2} =1(8)2/3−1(4)1/2= \frac{1}{(8)^{2/3}} - \frac{1}{(4)^{1/2}} =1(23)2/3−1(22)1/2= \frac{1}{(2^3)^{2/3}} - \frac{1}{(2^2)^{1/2}} =122−121= \frac{1}{2^2} - \frac{1}{2^1} =14−12=14−24=−14= \frac{1}{4} - \frac{1}{2} = \frac{1}{4} - \frac{2}{4} = -\frac{1}{4}