Question
Question: $\lim_{x \to 1} \frac{\log x}{x-1}=$...
limx→1x−1logx=
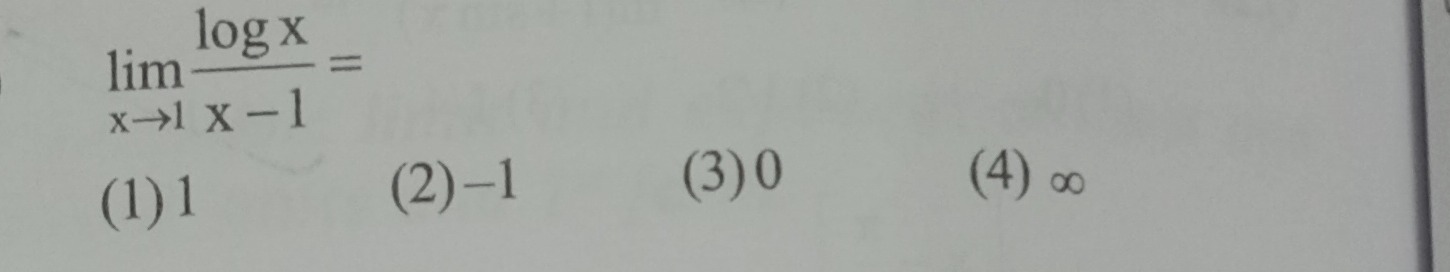
1
-1
0
∞
1
Solution
The given limit is limx→1x−1logx.
First, let's check the form of the limit by substituting x=1: Numerator: logx→log1=0 Denominator: x−1→1−1=0 The limit is of the indeterminate form 00.
We can evaluate this limit using L'Hôpital's Rule or by using a standard limit formula.
Method 1: Using L'Hôpital's Rule
Since the limit is of the 00 form, we can apply L'Hôpital's Rule, which states that if limx→cg(x)f(x) is of the form 00 or ∞∞, then limx→cg(x)f(x)=limx→cg′(x)f′(x), provided the latter limit exists.
Let f(x)=logx and g(x)=x−1. Then, find their derivatives: f′(x)=dxd(logx)=x1 g′(x)=dxd(x−1)=1
Now, apply L'Hôpital's Rule:
x→1limx−1logx=x→1lim1x1 =x→1limx1Substitute x=1 into the expression:
=11=1Method 2: Using Standard Limit Formula
Let x−1=h. As x→1, h→0. From x−1=h, we get x=1+h. Substitute these into the limit expression:
x→1limx−1logx=h→0limhlog(1+h)This is a standard limit formula, which is known to be equal to 1:
h→0limhlog(1+h)=1Both methods yield the same result.
