Question
Question: $\lim_{x \to 0}\frac{e^x-1-x}{x^2}$...
limx→0x2ex−1−x
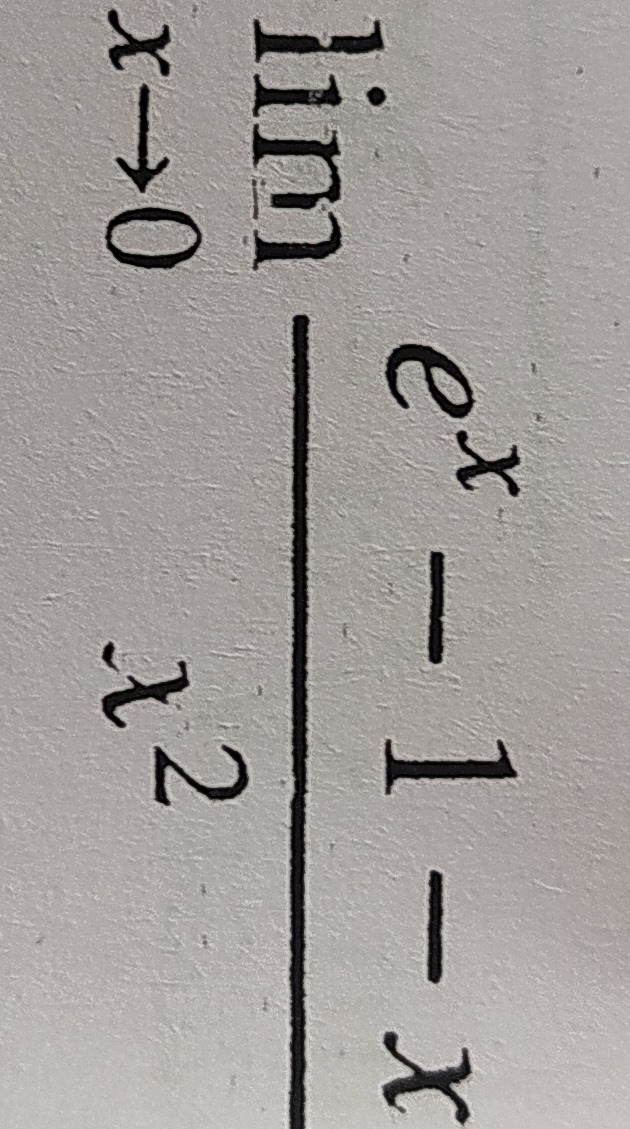
Answer
1/2
Explanation
Solution
The limit is in the indeterminate form 00 as x→0. Using L'Hôpital's Rule, we differentiate the numerator and the denominator. After the first application, we get limx→02xex−1, which is still 00. Applying L'Hôpital's Rule again, we get limx→02ex. Evaluating this limit gives 2e0=21.
Alternatively, using the Taylor series expansion ex=1+x+2!x2+…, the expression simplifies to 21+6x+…, and the limit as x→0 is 21.
