Solveeit Logo
Login

Question

Question: $\lim_{x \to 0^+} x \ln x$...

lim⁡x→0+xln⁡x\lim_{x \to 0^+} x \ln x

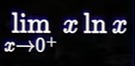
Answer

0

Explanation

Solution

The limit lim⁡x→0+xln⁡x\lim_{x \to 0^+} x \ln x is an indeterminate form 0×(−∞)0 \times (-\infty).

Rewrite it as lim⁡x→0+ln⁡x1/x\lim_{x \to 0^+} \frac{\ln x}{1/x}, which is an −∞∞\frac{-\infty}{\infty} form.

Apply L'Hôpital's Rule by differentiating the numerator and denominator: lim⁡x→0+1/x−1/x2\lim_{x \to 0^+} \frac{1/x}{-1/x^2}.

Simplify the expression to lim⁡x→0+(−x)\lim_{x \to 0^+} (-x).

Evaluating this limit gives 00.