Question
Question: $\lim_{x \to 0} \left( \sin^2\frac{\pi}{2-ax} \right)^{\sec^2\frac{\pi}{2-bx}}$...
limx→0(sin22−axπ)sec22−bxπ
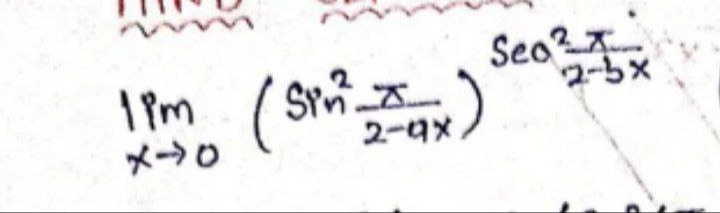
Answer
e−b2a2
Explanation
Solution
The limit is of the indeterminate form 1∞. Using the property limx→c[f(x)]g(x)=elimx→cg(x)[f(x)−1], we identify f(x)=sin2(2−axπ) and g(x)=sec2(2−bxπ). By applying trigonometric identities sin(2π−θ)=cosθ and secθ=1/cosθ, we simplify f(x) to cos2(ax) and g(x) to sin2(bx)1. Then f(x)−1=cos2(ax)−1=−sin2(ax). The exponent limit becomes limx→0sin2(bx)1(−sin2(ax))=limx→0−sin2(bx)sin2(ax). Using the standard limit limu→0usinu=1, this simplifies to −b2a2. Therefore, the original limit is e−a2/b2.
