Question
Question: $\lim_{x \to 0} \frac{\tan(\tan x) - \sin(\sin x)}{\tan x - \sin x}$...
limx→0tanx−sinxtan(tanx)−sin(sinx)
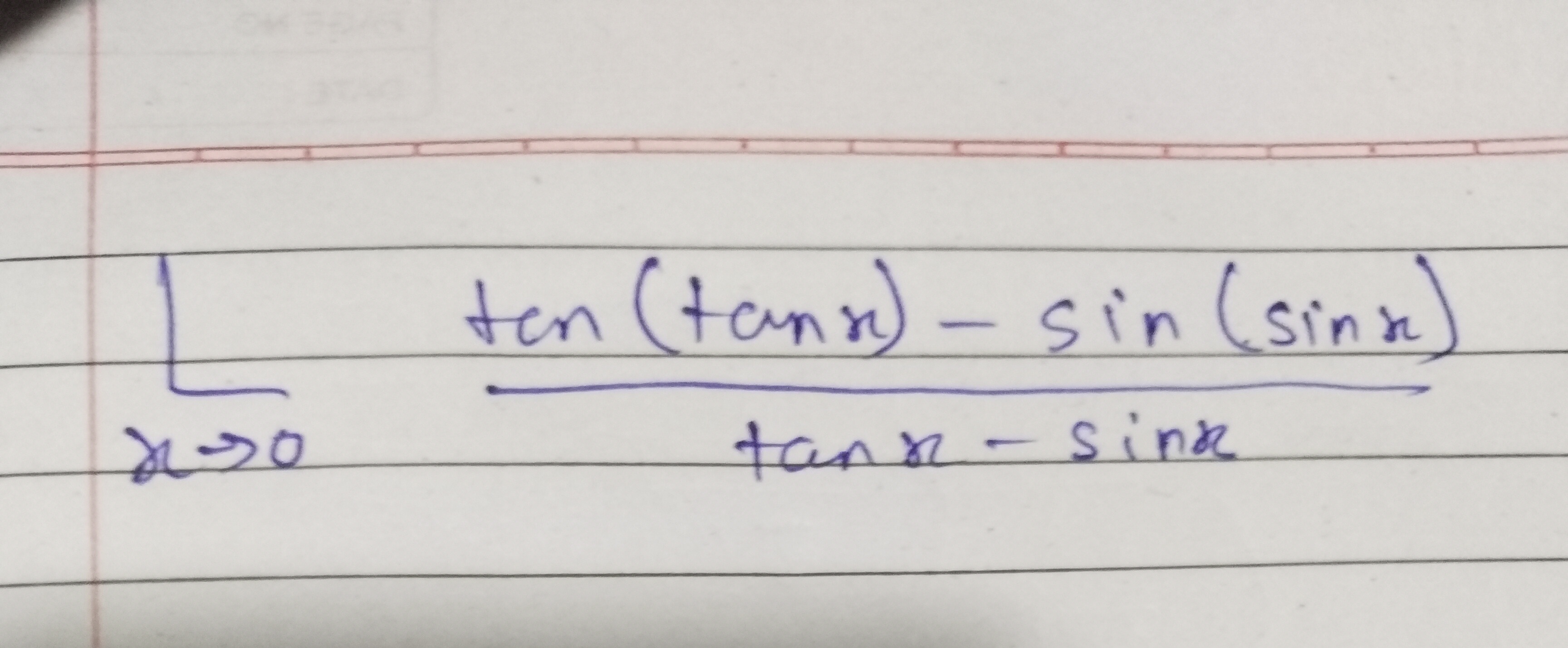
1
2
1/2
3/2
2
Solution
To evaluate the limit limx→0tanx−sinxtan(tanx)−sin(sinx), we can utilize Taylor series expansions for tanx and sinx around x=0.
The Taylor series expansions are: tanx=x+3x3+O(x5) sinx=x−6x3+O(x5)
First, we find the Taylor expansion for the denominator: tanx−sinx=(x+3x3+O(x5))−(x−6x3+O(x5)) tanx−sinx=3x3+6x3+O(x5)=62x3+x3+O(x5)=63x3+O(x5)=2x3+O(x5).
Next, we find the Taylor expansion for the numerator, tan(tanx)−sin(sinx). For tan(tanx): Let u=tanx=x+3x3+O(x5). Using tanu=u+3u3+O(u5): tan(tanx)=tan(x+3x3+O(x5))=(x+3x3+O(x5))+31(x+3x3+O(x5))3+O(x5) tan(tanx)=x+3x3+31(x3)+O(x5)=x+32x3+O(x5).
For sin(sinx): Let v=sinx=x−6x3+O(x5). Using sinv=v−6v3+O(v5): sin(sinx)=sin(x−6x3+O(x5))=(x−6x3+O(x5))−61(x−6x3+O(x5))3+O(x5) sin(sinx)=x−6x3−61(x3)+O(x5)=x−62x3+O(x5)=x−3x3+O(x5).
Now, we find the expansion for the numerator: tan(tanx)−sin(sinx)=(x+32x3+O(x5))−(x−3x3+O(x5)) tan(tanx)−sin(sinx)=32x3+3x3+O(x5)=x3+O(x5).
Finally, we evaluate the limit: limx→0tanx−sinxtan(tanx)−sin(sinx)=limx→02x3+O(x5)x3+O(x5) Dividing the numerator and denominator by x3: limx→021+O(x2)1+O(x2)=211=2
