Question
Question: $\lim_{x \to 0} \frac{tan2024x - tan2022x - tan2x}{x^3}$...
limx→0x3tan2024x−tan2022x−tan2x
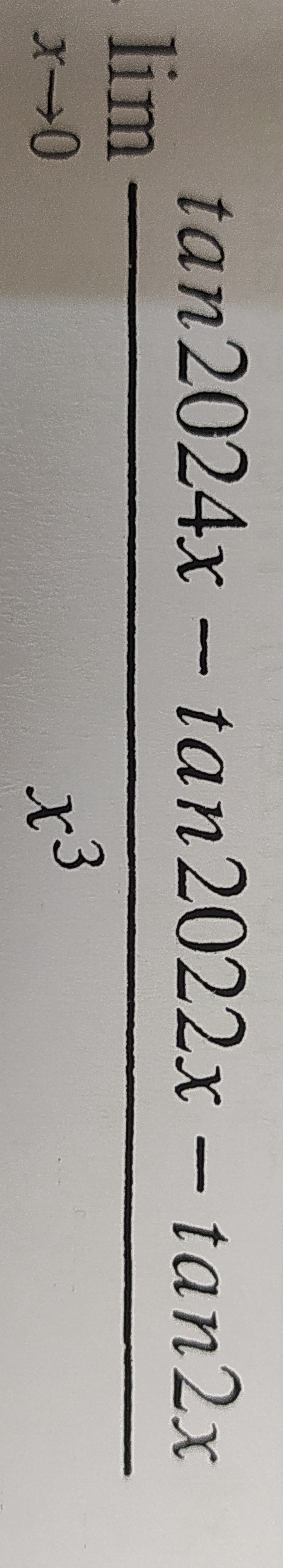
8185056
Solution
Let the given limit be L. We have L=limx→0x3tan(2024x)−tan(2022x)−tan(2x). This is a 00 form as x→0. We can use the Taylor series expansion of tanu around u=0. The Taylor series expansion for tanu up to the u3 term is tanu=u+3u3+O(u5).
Let a=2024, b=2022, and c=2. The expression is x3tan(ax)−tan(bx)−tan(cx). We notice that a=b+c, i.e., 2024=2022+2. This relationship will simplify the calculation.
Using the Taylor expansion: tan(ax)=ax+3(ax)3+O((ax)5)=ax+3a3x3+O(x5) tan(bx)=bx+3(bx)3+O((bx)5)=bx+3b3x3+O(x5) tan(cx)=cx+3(cx)3+O((cx)5)=cx+3c3x3+O(x5)
Substitute these expansions into the numerator: Numerator =(ax+3a3x3+O(x5))−(bx+3b3x3+O(x5))−(cx+3c3x3+O(x5)) Numerator =(ax−bx−cx)+(3a3x3−3b3x3−3c3x3)+O(x5) Numerator =(a−b−c)x+3a3−b3−c3x3+O(x5)
Since a=b+c, we have a−b−c=0. So, the term with x vanishes: Numerator =(0)x+3a3−b3−c3x3+O(x5) Numerator =3a3−b3−c3x3+O(x5)
Now, divide the numerator by x3: x3Numerator=x33a3−b3−c3x3+O(x5)=3a3−b3−c3+O(x2)
Take the limit as x→0: L=limx→0(3a3−b3−c3+O(x2))=3a3−b3−c3
We need to calculate a3−b3−c3 with a=2024, b=2022, c=2. Since a=b+c, we can use the identity: if x+y+z=0, then x3+y3+z3=3xyz. Let x=a, y=−b, z=−c. Then x+y+z=a−b−c=0. So, a3+(−b)3+(−c)3=3(a)(−b)(−c). a3−b3−c3=3abc.
Substitute this into the limit expression: L=33abc=abc.
Now, substitute the values of a, b, and c: L=2024×2022×2. L=2024×(2022×2) L=2024×4044.
Calculate the product: 2024×4044=(2000+24)×(4000+44) =2000×4000+2000×44+24×4000+24×44 =8000000+88000+96000+1056 =8000000+184000+1056 =8184000+1056 =8185056.
Thus, the limit is 8185056.
