Question
Question: $\lim_{x \to 0} \frac{\sin(6x^2)}{ln \cos(2x^2 - x)}$ is equal to...
limx→0lncos(2x2−x)sin(6x2) is equal to
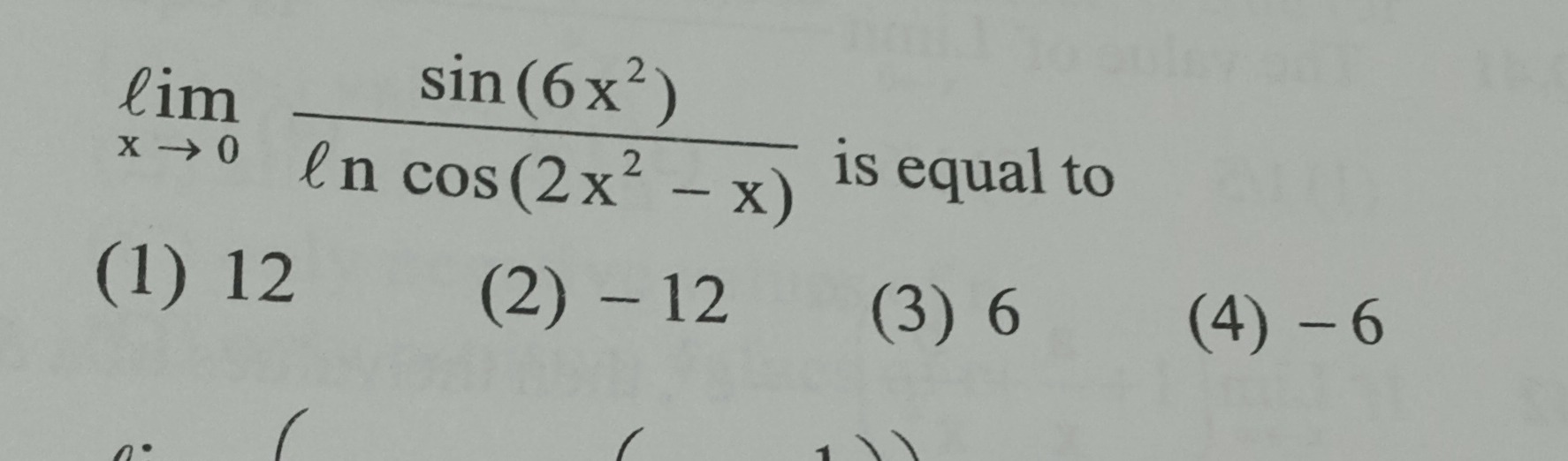
12
-12
6
-6
-12
Solution
To evaluate the limit limx→0lncos(2x2−x)sin(6x2), we first check the form of the limit by substituting x=0:
Numerator: sin(6(0)2)=sin(0)=0
Denominator: lncos(2(0)2−0)=lncos(0)=ln(1)=0
The limit is of the indeterminate form 00. We can use standard limit formulas.
We use the following standard limits and approximations for small y:
-
limy→0ysiny=1⟹siny≈y
-
limy→0yln(1+y)=1⟹ln(1+y)≈y
-
limy→0y21−cosy=21⟹1−cosy≈2y2⟹cosy−1≈−2y2
Let's apply these to the given expression:
Numerator:
sin(6x2)
As x→0, 6x2→0. Using approximation siny≈y:
sin(6x2)≈6x2
Denominator:
lncos(2x2−x)
We rewrite cos(2x2−x) as 1+(cos(2x2−x)−1).
Let Y=cos(2x2−x)−1. As x→0, 2x2−x→0, so cos(2x2−x)→cos(0)=1, which means Y→0.
Using approximation ln(1+Y)≈Y:
lncos(2x2−x)=ln(1+(cos(2x2−x)−1))≈cos(2x2−x)−1
Now, we need to approximate cos(2x2−x)−1.
Let θ=2x2−x. As x→0, θ→0.
Using approximation cosθ−1≈−2θ2:
cos(2x2−x)−1≈−2(2x2−x)2
Substitute these approximations back into the limit expression:
limx→0lncos(2x2−x)sin(6x2)=limx→0−2(2x2−x)26x2
Simplify the denominator:
(2x2−x)2=(x(2x−1))2=x2(2x−1)2
So the limit becomes:
limx→0−2x2(2x−1)26x2
Cancel out x2 from the numerator and denominator (since x=0 as x→0):
=limx→0−2(2x−1)26
Now, substitute x=0:
=−2(2(0)−1)26
=−2(−1)26
=−216
=6×(−2)
=−12
The final answer is −12.
