Question
Question: $\lim_{x \to 0} \frac{(\cos x)^{\csc^2x}-e^{\csc^2x(\cos x -1)}}{x^2}$...
limx→0x2(cosx)csc2x−ecsc2x(cosx−1)
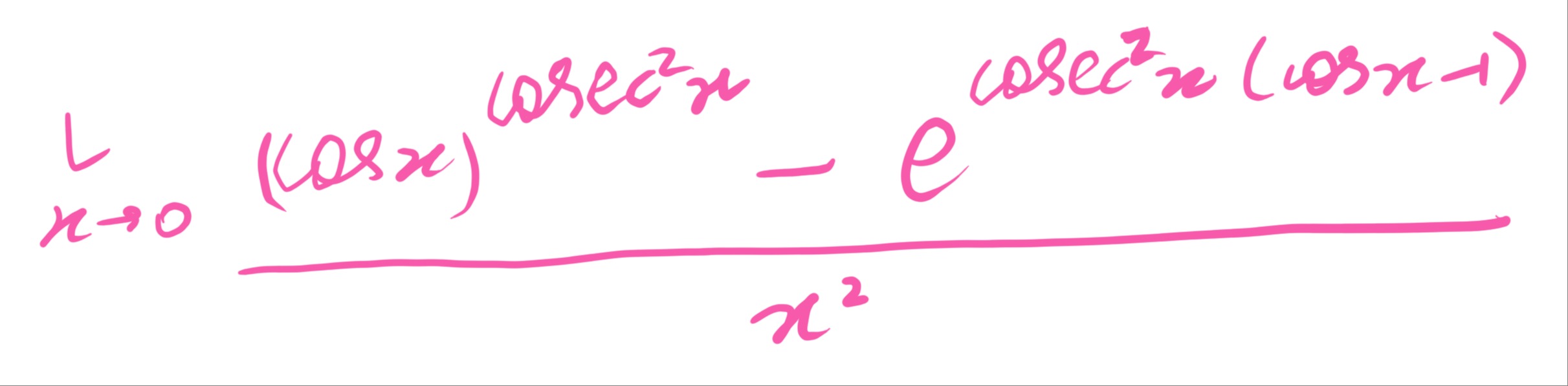
−8e1
Solution
The given limit is limx→0x2(cosx)csc2x−ecsc2x(cosx−1). This is of the indeterminate form 00. We will use Maclaurin series expansions for the functions involved.
We need the series expansions for cosx, sinx, eu, and ln(1+u) around x=0. cosx=1−2!x2+4!x4−O(x6)=1−2x2+24x4−O(x6) sinx=x−3!x3+O(x5)=x−6x3+O(x5) eu=1+u+2!u2+O(u3) ln(1+u)=u−2u2+3u3−O(u4)
First, let's find the expansion for csc2x: sin2x=(x−6x3+O(x5))2=x2(1−6x2+O(x4))2=x2(1−62x2+O(x4))=x2(1−3x2+O(x4)) csc2x=sin2x1=x2(1−3x2+O(x4))1=x21(1−3x2+O(x4))−1 Using (1−u)−1=1+u+u2+…, we get: csc2x=x21(1+3x2+O(x4))
Now, let's analyze the exponent term that appears in both parts of the numerator: E=csc2x(cosx−1). cosx−1=−2x2+24x4−O(x6) E=x21(1+3x2+O(x4))(−2x2+24x4−O(x6)) E=(1+3x2+O(x4))(−21+24x2−O(x4)) E=−21+24x2−6x2+O(x4) E=−21+x2(241−244)+O(x4) E=−21−243x2+O(x4)=−21−8x2+O(x4)
Let's evaluate the second term in the numerator, B=ecsc2x(cosx−1)=eE: B=e−1/2−x2/8+O(x4)=e−1/2e−x2/8+O(x4) Using eu=1+u+O(u2): B=e−1/2(1+(−8x2+O(x4))+O(x4)) B=e−1/2(1−8x2+O(x4))
Now, let's evaluate the first term in the numerator, A=(cosx)csc2x. We can write A=ecsc2xln(cosx). Let F=csc2xln(cosx). First, expand ln(cosx): ln(cosx)=ln(1+(cosx−1)). Let u=cosx−1=−2x2+24x4−O(x6). Using ln(1+u)=u−2u2+O(u3): ln(cosx)=(−2x2+24x4)−21(−2x2)2+O(x6) ln(cosx)=−2x2+24x4−8x4+O(x6) ln(cosx)=−2x2+x4(241−243)+O(x6) ln(cosx)=−2x2−242x4+O(x6)=−2x2−12x4+O(x6)
Now, substitute this into F: F=x21(1+3x2+O(x4))(−2x2−12x4+O(x6)) F=(1+3x2+O(x4))(−21−12x2+O(x4)) F=−21−12x2−6x2+O(x4) F=−21+x2(−121−122)+O(x4) F=−21−123x2+O(x4)=−21−4x2+O(x4)
Now, A=eF: A=e−1/2−x2/4+O(x4)=e−1/2e−x2/4+O(x4) Using eu=1+u+O(u2): A=e−1/2(1+(−4x2+O(x4))+O(x4)) A=e−1/2(1−4x2+O(x4))
Finally, substitute A and B back into the limit expression: limx→0x2A−B=limx→0x2e−1/2(1−4x2+O(x4))−e−1/2(1−8x2+O(x4)) =limx→0x2e−1/2(1−4x2−1+8x2+O(x4)) =limx→0x2e−1/2(−82x2+8x2+O(x4)) =limx→0x2e−1/2(−8x2+O(x4)) =limx→0e−1/2(−81+O(x2)) =−81e−1/2
The final answer is −8e1.
Solution: The limit is of the form 00. We use Maclaurin series expansions.
- Expand csc2x: csc2x=x21(1+3x2+O(x4)).
- Expand the common exponent E=csc2x(cosx−1): cosx−1=−2x2+24x4−O(x6). E=x21(1+3x2+O(x4))(−2x2+24x4−O(x6))=−21−8x2+O(x4).
- Expand the second term ecsc2x(cosx−1)=eE: eE=e−1/2−x2/8+O(x4)=e−1/2(1−8x2+O(x4)).
- Expand the first term (cosx)csc2x=ecsc2xln(cosx). Let F=csc2xln(cosx). ln(cosx)=ln(1+(cosx−1))=(cosx−1)−2(cosx−1)2+O((cosx−1)3). ln(cosx)=(−2x2+24x4)−21(−2x2)2+O(x6)=−2x2−12x4+O(x6). F=x21(1+3x2+O(x4))(−2x2−12x4+O(x6))=−21−4x2+O(x4). So, (cosx)csc2x=eF=e−1/2−x2/4+O(x4)=e−1/2(1−4x2+O(x4)).
- Substitute these expansions into the limit: limx→0x2e−1/2(1−4x2+O(x4))−e−1/2(1−8x2+O(x4)) =limx→0x2e−1/2(1−4x2−1+8x2+O(x4)) =limx→0x2e−1/2(−8x2+O(x4))=−81e−1/2.
The final answer is −8e1.
