Question

$\lim_{x \to 0} \frac{(1+sinx)^{\frac{1}{2024}}+(1-tanx)^{\frac{1}{2024}}}{x^3}$

Answer 1

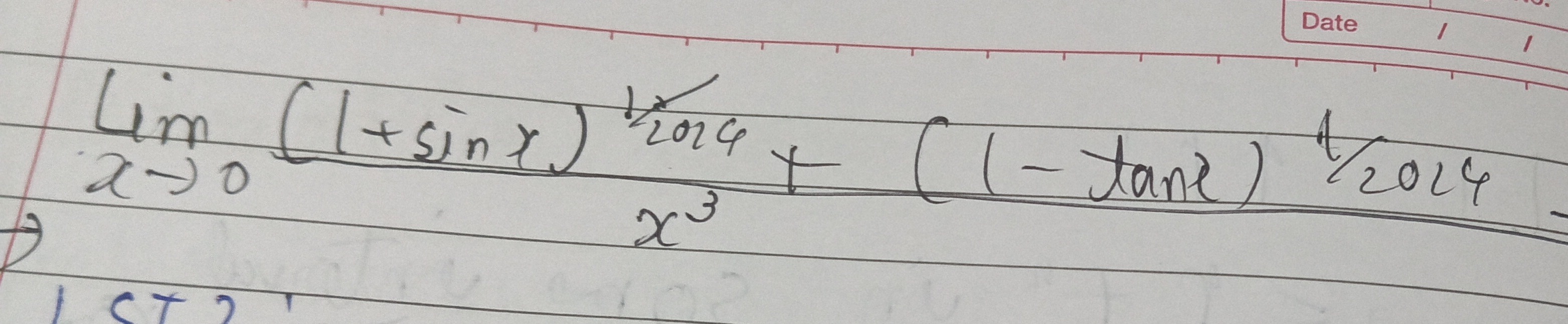
Does not exist

Answer 2

To evaluate the limit $\lim_{x \to 0} \frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}}{x^3}$, we first evaluate the numerator and the denominator as $x$ approaches $0$.

1. Evaluate the numerator as $x \to 0$:
   Let $N(x) = (1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}$.
   As $x \to 0$, $\sin x \to \sin 0 = 0$ and $\tan x \to \tan 0 = 0$.
   So, $N(x) \to (1+0)^{\frac{1}{2024}} + (1-0)^{\frac{1}{2024}} = 1^{\frac{1}{2024}} + 1^{\frac{1}{2024}} = 1+1=2$.

2. Evaluate the denominator as $x \to 0$:
   Let $D(x) = x^3$.
   As $x \to 0$, $D(x) \to 0^3 = 0$.

3. Determine the form of the limit:
   The limit is of the form $\frac{2}{0}$. This indicates that the limit will be either $+\infty$, $-\infty$, or does not exist. To determine this, we need to examine the one-sided limits.

4. Analyze the one-sided limits:

   • Right-hand limit (RHL): As $x \to 0^+$, $x$ is a small positive number. Therefore, $x^3$ is also a small positive number ($x^3 \to 0^+$). The numerator approaches a positive value, 2.
     $\lim_{x \to 0^+} \frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}}{x^3} = \frac{2}{0^+} = +\infty$.

   • Left-hand limit (LHL): As $x \to 0^-$, $x$ is a small negative number. Therefore, $x^3$ is also a small negative number ($x^3 \to 0^-$). The numerator approaches a positive value, 2.
     $\lim_{x \to 0^-} \frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}}{x^3} = \frac{2}{0^-} = -\infty$.

5. Conclusion:
   Since the right-hand limit ($+\infty$) and the left-hand limit ($-\infty$) are not equal, the limit does not exist.

Explanation of the solution:
The numerator approaches 2 as $x \to 0$, while the denominator approaches 0. This results in a limit of the form $\frac{2}{0}$. Evaluating the one-sided limits, we find that the right-hand limit is $+\infty$ (since $x^3 \to 0^+$) and the left-hand limit is $-\infty$ (since $x^3 \to 0^-$). As the one-sided limits are not equal, the overall limit does not exist.