Question
Question: $\lim_{x \to 0} \frac{(1+sinx)^{\frac{1}{2024}} - (1 - sinx)^{\frac{1}{2024}}}{x}$...
limx→0x(1+sinx)20241−(1−sinx)20241
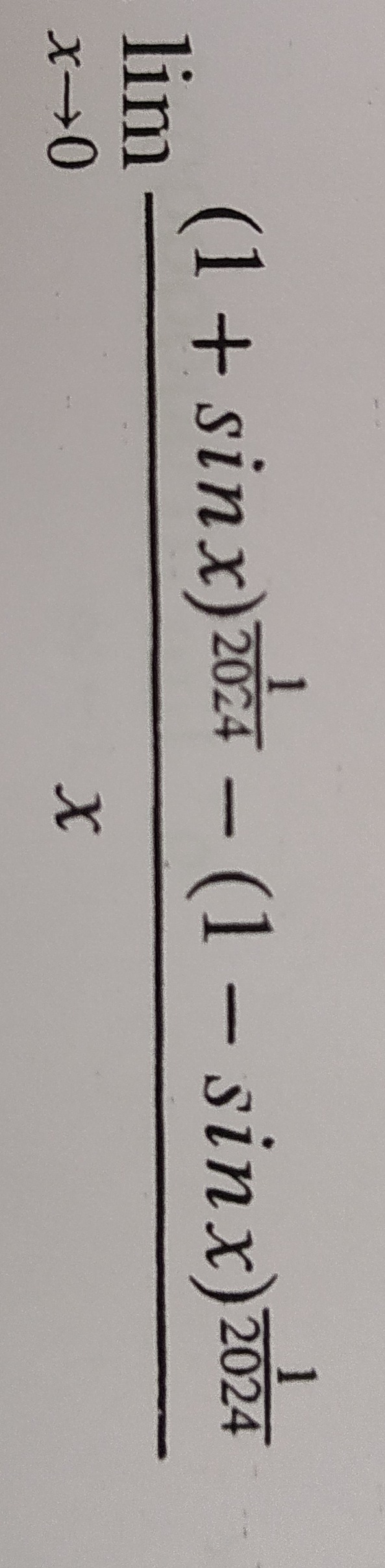
1/1012
Solution
The given limit is of the form 00 as x→0. We can solve this using L'Hopital's Rule, standard limit formulas, or binomial approximation.
Method 1: Using L'Hopital's Rule Let f(x)=(1+sinx)20241−(1−sinx)20241 and g(x)=x. Then f′(x)=dxd[(1+sinx)20241−(1−sinx)20241] Using the chain rule, dudun=nun−1dxdu: f′(x)=20241(1+sinx)20241−1⋅cosx−20241(1−sinx)20241−1⋅(−cosx) f′(x)=20241(1+sinx)−20242023cosx+20241(1−sinx)−20242023cosx g′(x)=dxd(x)=1
Now, apply L'Hopital's Rule: limx→0g′(x)f′(x)=limx→0[20241(1+sinx)−20242023cosx+20241(1−sinx)−20242023cosx] Substitute x=0: =20241(1+sin0)−20242023cos0+20241(1−sin0)−20242023cos0 =20241(1+0)−20242023⋅1+20241(1−0)−20242023⋅1 =20241(1)+20241(1) =20242=10121
Method 2: Using Standard Limit Formula and Binomial Approximation We know the standard limit formula: limy→0y(1+y)n−1=n. Let n=20241. The expression can be rewritten as: limx→0x[(1+sinx)n−1]−[(1−sinx)n−1] =limx→0x(1+sinx)n−1−limx→0x(1−sinx)n−1
For the first term: limx→0x(1+sinx)n−1=limx→0sinx(1+sinx)n−1⋅xsinx As x→0, sinx→0. Let y=sinx. =limy→0y(1+y)n−1⋅limx→0xsinx =n⋅1=n
For the second term: limx→0x(1−sinx)n−1=limx→0−sinx(1+(−sinx))n−1⋅x−sinx As x→0, −sinx→0. Let z=−sinx. =limz→0z(1+z)n−1⋅limx→0x−sinx =n⋅(−1)=−n
Combining the two terms: The limit is n−(−n)=2n. Substitute n=20241: 2⋅20241=20242=10121
Alternatively, using binomial approximation (1+u)n≈1+nu for small u: As x→0, sinx→0. (1+sinx)20241≈1+20241sinx (1−sinx)20241≈1+20241(−sinx)=1−20241sinx
Substitute these into the expression: limx→0x(1+20241sinx)−(1−20241sinx) =limx→0x1+20241sinx−1+20241sinx =limx→0x2⋅20241sinx =limx→010121xsinx Since limx→0xsinx=1: =10121⋅1=10121
All methods yield the same result.
