Question

$\lim_{x \to 0} (\cos x)^{\csc^2 x}$

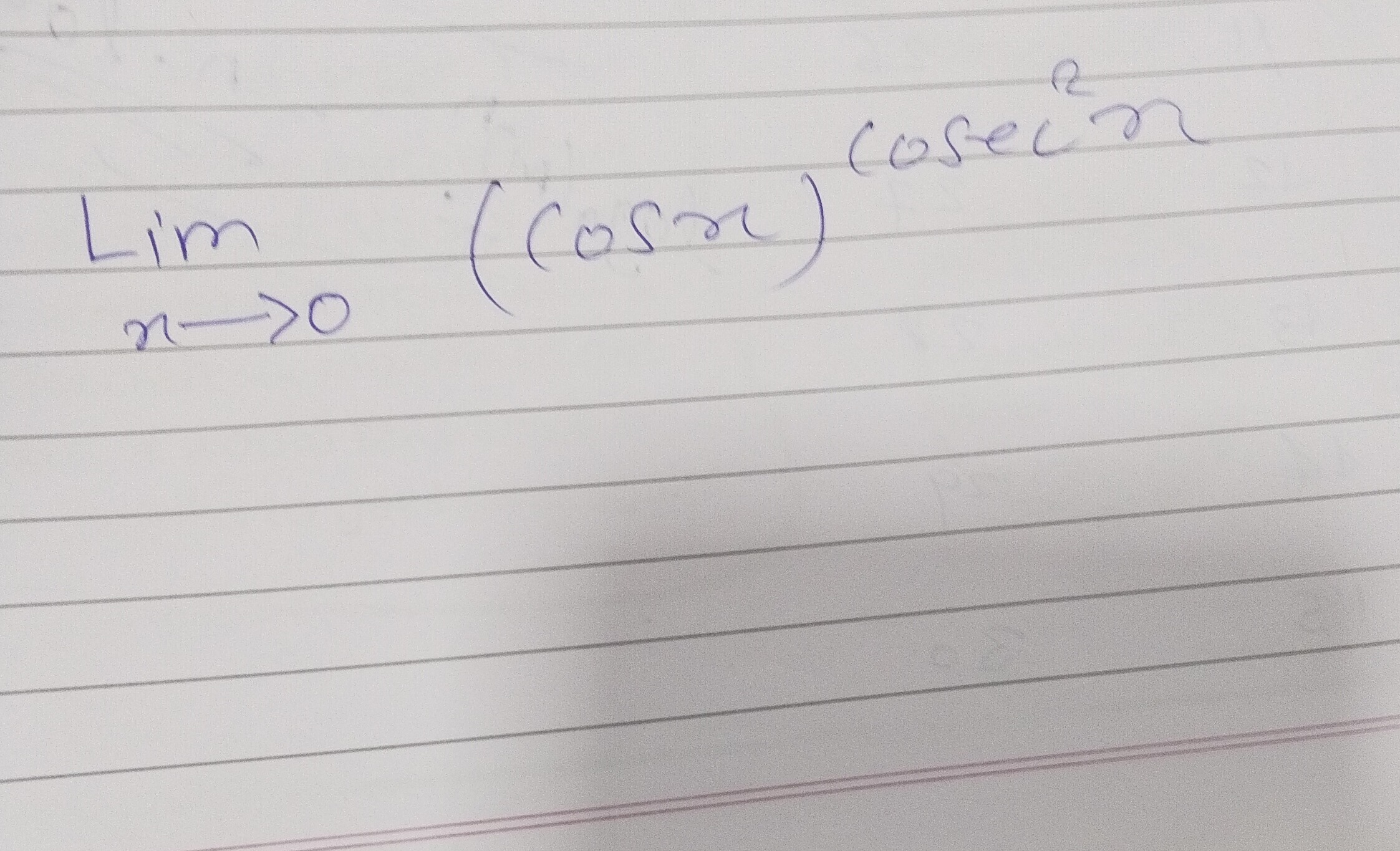
Answer 1

$e^{-1/2}$

Answer 2

The limit is of the indeterminate form $1^\infty$. We use the property that if $\lim_{x \to a} [f(x)]^{g(x)}$ is $1^\infty$, then it equals $e^{\lim_{x \to a} g(x) [f(x) - 1]}$. We evaluate the exponent limit $\lim_{x \to 0} \csc^2 x (\cos x - 1) = \lim_{x \to 0} \frac{\cos x - 1}{\sin^2 x}$. This is of the form $\frac{0}{0}$. By dividing numerator and denominator by $x^2$ and using standard limits $\lim_{x \to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2}$ and $\lim_{x \to 0} \frac{\sin x}{x} = 1$, we find the exponent limit to be $-\frac{1}{2}$. Therefore, the original limit is $e^{-1/2}$.