Question

\lim_{n\to+\infty} n^2 \int_{0}^{\frac{1}{n}} \frac{e^x-1}{1+n^4x^4}dx

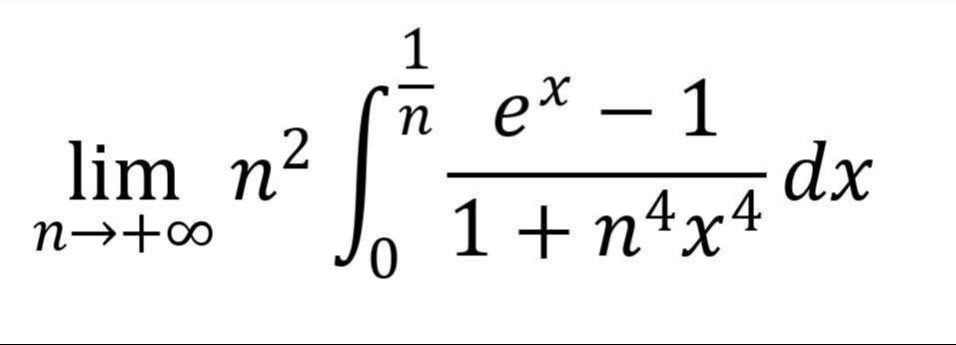
Answer 1

\frac{\pi}{8}

Answer 2

Let $x = u/n$, so $dx = du/n$. The integral becomes: $L = \lim_{n\to+\infty} n^2 \int_{0}^{1} \frac{e^{u/n}-1}{1+n^4(u/n)^4} \frac{du}{n} = \lim_{n\to+\infty} n \int_{0}^{1} \frac{e^{u/n}-1}{1+u^4} du$. Using the Taylor expansion $e^z - 1 = z + O(z^2)$, we have $e^{u/n}-1 = u/n + O(1/n^2)$. So, $L = \lim_{n\to+\infty} n \int_{0}^{1} \frac{u/n + O(1/n^2)}{1+u^4} du = \lim_{n\to+\infty} \int_{0}^{1} \frac{u}{1+u^4} du + \lim_{n\to+\infty} \int_{0}^{1} \frac{O(1/n)}{1+u^4} du$. The second term goes to 0 as $n \to \infty$. The first term is $\int_{0}^{1} \frac{u}{1+u^4} du$. Let $v = u^2$, $dv = 2u\,du$. $\int_{0}^{1} \frac{1}{1+v^2} \frac{dv}{2} = \frac{1}{2} [\arctan(v)]_{0}^{1} = \frac{1}{2} (\arctan(1) - \arctan(0)) = \frac{1}{2} (\frac{\pi}{4} - 0) = \frac{\pi}{8}$. Thus, $L = \frac{\pi}{8}$.