Solveeit Logo
Login

Question

Question: $\lim_{n \to \infty} n \sin(2\pi e n!)$...

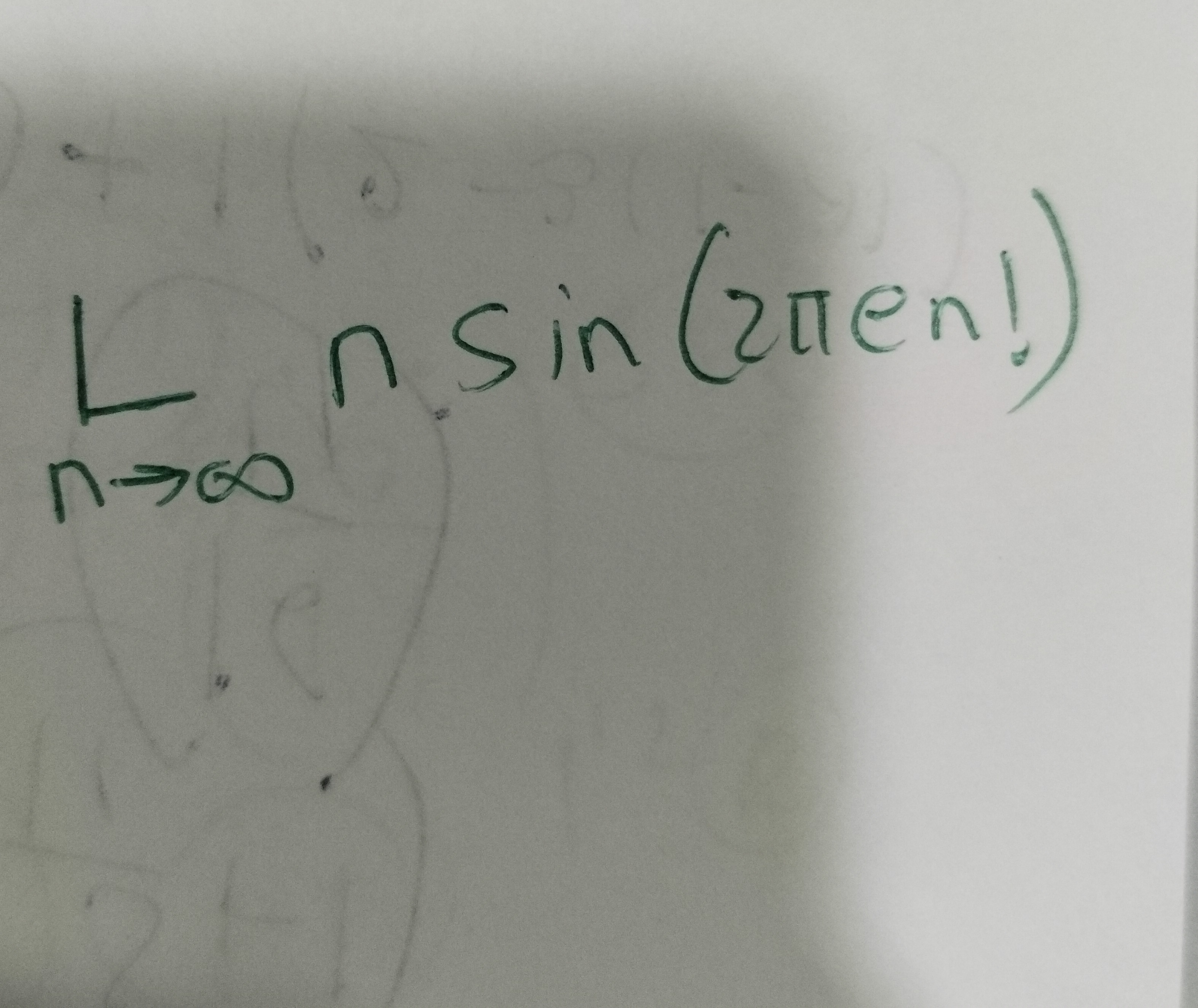
lim⁡n→∞nsin⁡(2πen!)\lim_{n \to \infty} n \sin(2\pi e n!)

Answer

2\pi

Explanation

Solution

The limit can be evaluated by using the Taylor series expansion of ee. We know that e=∑k=0∞1k!e = \sum_{k=0}^{\infty} \frac{1}{k!}. Multiplying by n!n!, we get e⋅n!=n!∑k=0∞1k!=∑k=0∞n!k!e \cdot n! = n! \sum_{k=0}^{\infty} \frac{1}{k!} = \sum_{k=0}^{\infty} \frac{n!}{k!}. We can split this sum into an integer part In=∑k=0nn!k!I_n = \sum_{k=0}^{n} \frac{n!}{k!} and a remainder part Rn=∑k=n+1∞n!k!R_n = \sum_{k=n+1}^{\infty} \frac{n!}{k!}. So, e⋅n!=In+Rne \cdot n! = I_n + R_n. For n≥1n \ge 1, InI_n is an integer. The remainder term RnR_n can be written as: Rn=n!(n+1)!+n!(n+2)!+⋯=1n+1+1(n+1)(n+2)+…R_n = \frac{n!}{(n+1)!} + \frac{n!}{(n+2)!} + \dots = \frac{1}{n+1} + \frac{1}{(n+1)(n+2)} + \dots We can bound RnR_n for n≥1n \ge 1: 0<Rn<1n+1+1(n+1)2+1(n+1)3+⋯=1n+11−1n+1=1n0 < R_n < \frac{1}{n+1} + \frac{1}{(n+1)^2} + \frac{1}{(n+1)^3} + \dots = \frac{\frac{1}{n+1}}{1 - \frac{1}{n+1}} = \frac{1}{n}. As n→∞n \to \infty, Rn→0R_n \to 0 by the Squeeze Theorem.

Now consider the sine term: sin⁡(2πen!)=sin⁡(2π(In+Rn))=sin⁡(2πIn+2πRn)\sin(2\pi e n!) = \sin(2\pi (I_n + R_n)) = \sin(2\pi I_n + 2\pi R_n). Since InI_n is an integer, sin⁡(2πIn+2πRn)=sin⁡(2πRn)\sin(2\pi I_n + 2\pi R_n) = \sin(2\pi R_n).

The limit becomes: L=lim⁡n→∞nsin⁡(2πRn)L = \lim_{n \to \infty} n \sin(2\pi R_n). As n→∞n \to \infty, Rn→0R_n \to 0, so we can use the limit lim⁡x→0sin⁡xx=1\lim_{x \to 0} \frac{\sin x}{x} = 1. L=lim⁡n→∞n(2πRn⋅sin⁡(2πRn)2πRn)=2πlim⁡n→∞(nRn)⋅lim⁡n→∞sin⁡(2πRn)2πRnL = \lim_{n \to \infty} n \left(2\pi R_n \cdot \frac{\sin(2\pi R_n)}{2\pi R_n}\right) = 2\pi \lim_{n \to \infty} (n R_n) \cdot \lim_{n \to \infty} \frac{\sin(2\pi R_n)}{2\pi R_n}. Since lim⁡n→∞sin⁡(2πRn)2πRn=1\lim_{n \to \infty} \frac{\sin(2\pi R_n)}{2\pi R_n} = 1, we have L=2πlim⁡n→∞nRnL = 2\pi \lim_{n \to \infty} n R_n.

Now we evaluate lim⁡n→∞nRn\lim_{n \to \infty} n R_n: nRn=n(1n+1+1(n+1)(n+2)+… )=nn+1+n(n+1)(n+2)+…n R_n = n \left(\frac{1}{n+1} + \frac{1}{(n+1)(n+2)} + \dots \right) = \frac{n}{n+1} + \frac{n}{(n+1)(n+2)} + \dots The first term nn+1→1\frac{n}{n+1} \to 1 as n→∞n \to \infty. The sum of the remaining terms can be bounded: 0<n(n+1)(n+2)+n(n+1)(n+2)(n+3)+⋯<n(n+1)2+n(n+1)3+⋯=n(n+1)21−1n+1=n(n+1)2⋅n+1n=1n+10 < \frac{n}{(n+1)(n+2)} + \frac{n}{(n+1)(n+2)(n+3)} + \dots < \frac{n}{(n+1)^2} + \frac{n}{(n+1)^3} + \dots = \frac{\frac{n}{(n+1)^2}}{1 - \frac{1}{n+1}} = \frac{n}{(n+1)^2} \cdot \frac{n+1}{n} = \frac{1}{n+1}. As n→∞n \to \infty, this sum tends to 0. Thus, lim⁡n→∞nRn=1\lim_{n \to \infty} n R_n = 1.

Finally, L=2π×1=2πL = 2\pi \times 1 = 2\pi.