Question

$\lim_{n \to \infty} n \sin(2\pi e n!)$

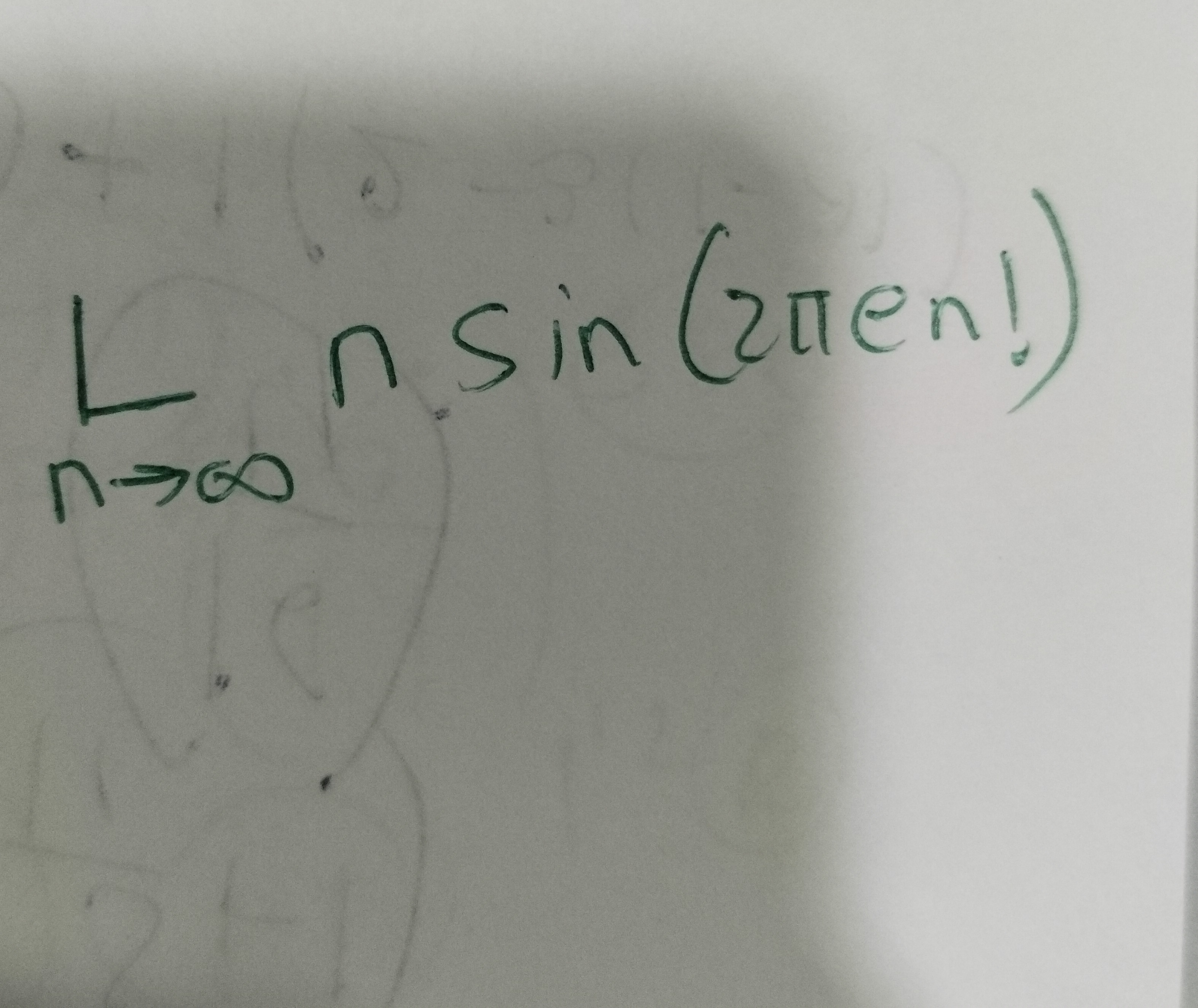
Answer 1

2\pi

Answer 2

1. Express $e n!$ as the sum of an integer $I_n$ and a remainder $R_n = \sum_{k=n+1}^{\infty} \frac{n!}{k!}$.
2. Use $\sin(2\pi e n!) = \sin(2\pi R_n)$ since $I_n$ is an integer.
3. Bound $R_n$: $\frac{1}{n+1} < R_n < \frac{1}{n}$ for $n \ge 1$, showing $R_n \to 0$ as $n \to \infty$.
4. Apply $\lim_{x\to 0} \frac{\sin x}{x} = 1$ to $\sin(2\pi R_n)$, reducing the limit to $2\pi \lim_{n \to \infty} n R_n$.
5. Bound $n R_n$: $\frac{n}{n+1} < n R_n < 1$ for $n \ge 1$.
6. By the Squeeze Theorem, $\lim_{n \to \infty} n R_n = 1$.
7. The final answer is $2\pi \times 1 = 2\pi$.