Question
Question: $\lim_{n \to \infty} n! \left( \prod_{K=1}^{n} \tan^{-1} \frac{1}{1+K+K^2} \right) =$...
limn→∞n!(∏K=1ntan−11+K+K21)=
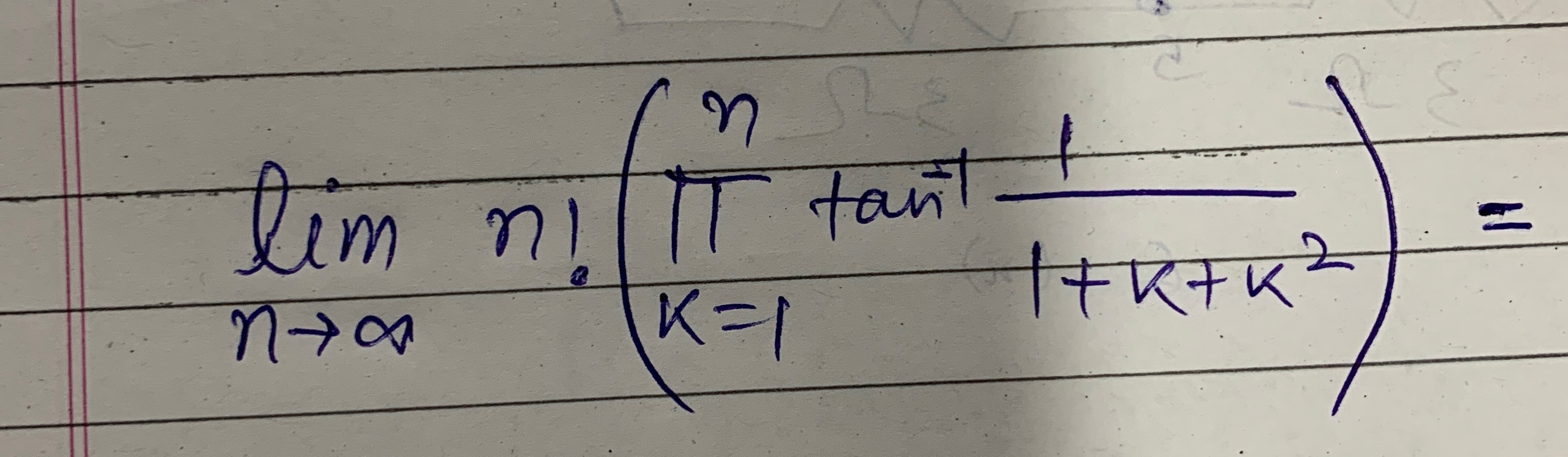
0
Solution
Let the given limit be L. The expression is L=limn→∞n!(∏K=1ntan−11+K+K21)
Let the term inside the product be aK=tan−11+K+K21. We use the identity tan−1x−tan−1y=tan−11+xyx−y. Let x=K+1 and y=K. Then x−y=(K+1)−K=1 and xy=K(K+1). So, tan−1(K+1)−tan−1K=tan−11+(K+1)K(K+1)−K=tan−11+K+K21. Thus, aK=tan−1(K+1)−tan−1K.
The product is Pn=∏K=1naK=∏K=1n(tan−1(K+1)−tan−1K). We need to evaluate the limit of n!Pn as n→∞. Consider the logarithm of the expression n!Pn: ln(n!Pn)=ln(n!)+lnPn=ln(n!)+∑K=1nlnaK.
For large K, aK=tan−1(K+1)−tan−1K is small. We can use the Taylor expansion of tan−1x for large x: tan−1x=2π−x1+3x31−5x51+…. aK=(2π−K+11+3(K+1)31−…)−(2π−K1+3K31−…) aK=(K1−K+11)−31(K31−(K+1)31)+… aK=K(K+1)1−31K3(K+1)33K2+3K+1+… aK=K2+K1−3(K6+3K5+3K4+K3)3K2+3K+1+… For large K, aK=K2(1+1/K)1−3K6(1+3/K+3/K2+1/K3)3K2(1+1/K+1/(3K2))+… aK=K21(1−1/K+O(1/K2))−K41(1+O(1/K))+… aK=K21−K31+O(K41).
Now consider lnaK for large K: lnaK=ln(K21−K31+O(K41))=ln(K21(1−1/K+O(1/K2))) lnaK=ln(1/K2)+ln(1−1/K+O(1/K2)) lnaK=−2lnK+(−1/K+O(1/K2))−21(−1/K+O(1/K2))2+O((−1/K)3) lnaK=−2lnK−1/K+O(1/K2).
Now sum lnaK from K=1 to n: ∑K=1nlnaK=∑K=1n(−2lnK−1/K+O(1/K2)) ∑K=1nlnaK=−2∑K=1nlnK−∑K=1n1/K+∑K=1nO(1/K2) ∑K=1nlnaK=−2ln(n!)−Hn+Cn, where Hn=∑K=1n1/K is the n-th harmonic number and Cn=∑K=1nO(1/K2). As n→∞, Cn converges to a constant C=∑K=1∞O(1/K2).
Now substitute this back into the expression for ln(n!Pn): ln(n!Pn)=ln(n!)+(−2ln(n!)−Hn+Cn)=−ln(n!)−Hn+Cn.
As n→∞, we use the asymptotic approximations: ln(n!)≈nlnn−n (by Stirling's formula) Hn≈lnn+γ, where γ is the Euler-Mascheroni constant. Cn→C.
So, limn→∞ln(n!Pn)=limn→∞(−ln(n!)−Hn+Cn) =limn→∞(−(nlnn−n+O(lnn))−(lnn+γ+o(1))+C+o(1)) =limn→∞(−nlnn+n−lnn−γ+C+O(lnn)) The dominant term is −nlnn, which tends to −∞ as n→∞. limn→∞ln(n!Pn)=−∞.
Therefore, the limit of the original expression is: L=limn→∞n!Pn=elimn→∞ln(n!Pn)=e−∞=0.
The final answer is 0.
