Question
Question: $\lim_{n \to \infty} \frac{(1^5+2^5+\dots+n^5)(1^8+2^8+\dots+n^8)}{1^{14}+2^{14}+\dots+n^{14}}$...
limn→∞114+214+⋯+n14(15+25+⋯+n5)(18+28+⋯+n8)
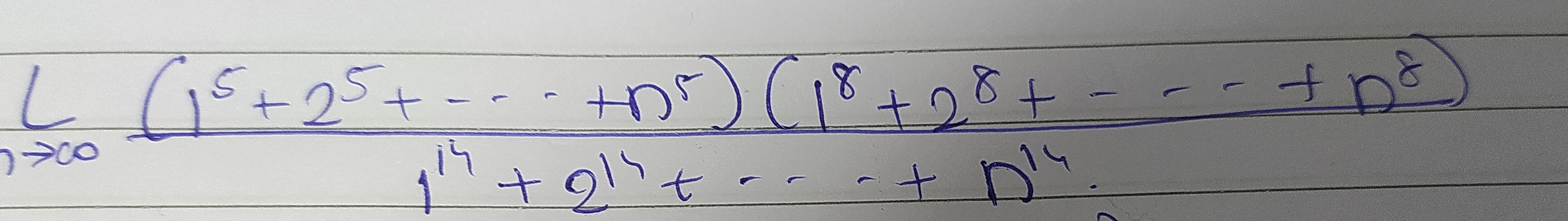
5/18
5/18
Solution
The problem asks us to evaluate the limit of an expression involving sums of powers of natural numbers.
The general formula for the sum of the p-th powers of the first n natural numbers is given by: ∑k=1nkp=1p+2p+⋯+np As n→∞, the dominant term in this sum is p+1np+1. More formally, we can state that: limn→∞np+1∑k=1nkp=p+11 This means that for large n, ∑k=1nkp≈p+1np+1.
Let's apply this approximation to each sum in the given expression:
-
For the sum 15+25+⋯+n5: Here p=5, so the sum is approximately 5+1n5+1=6n6.
-
For the sum 18+28+⋯+n8: Here p=8, so the sum is approximately 8+1n8+1=9n9.
-
For the sum 114+214+⋯+n14: Here p=14, so the sum is approximately 14+1n14+1=15n15.
Now, substitute these approximations into the limit expression: limn→∞114+214+⋯+n14(15+25+⋯+n5)(18+28+⋯+n8)=limn→∞(15n15)(6n6)(9n9)
Simplify the expression: =limn→∞15n156×9n6+9 =limn→∞15n1554n15 To simplify further, we can multiply the numerator by the reciprocal of the denominator: =limn→∞54n15×n1515 The n15 terms cancel out: =limn→∞5415 The limit is a constant value, which is 5415.
Finally, simplify the fraction 5415 by dividing both the numerator and the denominator by their greatest common divisor, which is 3: 54÷315÷3=185
The final answer is 185.
Explanation of the solution: The problem involves limits of sums of powers. The key is to use the asymptotic behavior of the sum of p-th powers of the first n natural numbers, ∑k=1nkp∼p+1np+1 as n→∞.
- Replace 15+25+⋯+n5 with its leading term 6n6.
- Replace 18+28+⋯+n8 with its leading term 9n9.
- Replace 114+214+⋯+n14 with its leading term 15n15.
- Substitute these into the limit expression: limn→∞(15n15)(6n6)(9n9)=limn→∞15n1554n15
- Simplify by canceling n15 and evaluating the constant fraction: 5415=185
