Question

$\lim_{→2} \frac{(sin2024)^x + (cos2024)^x - 1}{x-2}$

Answer 1

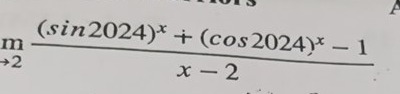
$(\sin 2024)^2 \ln(\sin 2024) + (\cos 2024)^2 \ln(\cos 2024)$

Answer 2

The problem asks to evaluate the limit:

$\lim_{x \to 2} \frac{(\sin 2024)^x + (\cos 2024)^x - 1}{x-2}$

Step 1: Check the form of the limit.

Let $f(x) = (\sin 2024)^x + (\cos 2024)^x - 1$. When $x=2$, the numerator is $f(2) = (\sin 2024)^2 + (\cos 2024)^2 - 1$. Using the identity $\sin^2\theta + \cos^2\theta = 1$, we have $f(2) = 1 - 1 = 0$. The denominator at $x=2$ is $2-2 = 0$. Since the limit is of the form $\frac{0}{0}$, we can use L'Hopital's Rule or the definition of the derivative.

Step 2: Apply the definition of the derivative.

The limit can be recognized as the definition of the derivative. Let $g(x) = (\sin 2024)^x + (\cos 2024)^x$. Then the expression in the limit is $\frac{g(x) - 1}{x-2}$. Since $g(2) = (\sin 2024)^2 + (\cos 2024)^2 = 1$, we can rewrite the limit as:

$\lim_{x \to 2} \frac{g(x) - g(2)}{x-2}$

This is precisely the definition of the derivative of $g(x)$ evaluated at $x=2$, i.e., $g'(2)$.

Step 3: Calculate the derivative $g'(x)$.

Let $a = \sin 2024$ and $b = \cos 2024$. So $g(x) = a^x + b^x$. The derivative of $c^x$ with respect to $x$ is $c^x \ln c$. Therefore, $g'(x) = \frac{d}{dx}(a^x) + \frac{d}{dx}(b^x) = a^x \ln a + b^x \ln b$.

Step 4: Evaluate $g'(2)$.

Substitute $x=2$ into $g'(x)$:

$g'(2) = a^2 \ln a + b^2 \ln b$

Substitute back $a = \sin 2024$ and $b = \cos 2024$:

$g'(2) = (\sin 2024)^2 \ln(\sin 2024) + (\cos 2024)^2 \ln(\cos 2024)$

Note: $2024$ radians is approximately $322 \times 2\pi + 0.425$ radians. This means $2024$ radians lies in the first quadrant, so $\sin 2024 > 0$ and $\cos 2024 > 0$. Thus, the logarithms are well-defined.