Question
Question: \(\lim _ { n \rightarrow \infty }\) \(\left[ \left( 1 + \frac { 1 } { n } \right) \left( 1 + \frac ...
limn→∞ [(1+n1)(1+n2)(1+n3)…(1+nn)]1/n =
A
4e
B
e4
C
e2
D
None of these
Answer
e4
Explanation
Solution
A = limn→∞[(1+n1)(1+n2)….(1+nn)]n1
log A =
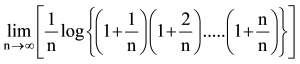


=  =
=  – ∫01x+11xdx
– ∫01x+11xdx
= log2 –  = log 2 –
= log 2 – 
= log 2 – [1 – log 2] = 2 log 2 – 1
log A = log 4 – 1
log A = log (4/e) ̃ A = 
