Question
Question: Lim 2ˣ (4tan⁻¹(1+2⁻ˣ)-π) is equal to x→∞...
Lim 2ˣ (4tan⁻¹(1+2⁻ˣ)-π) is equal to x→∞
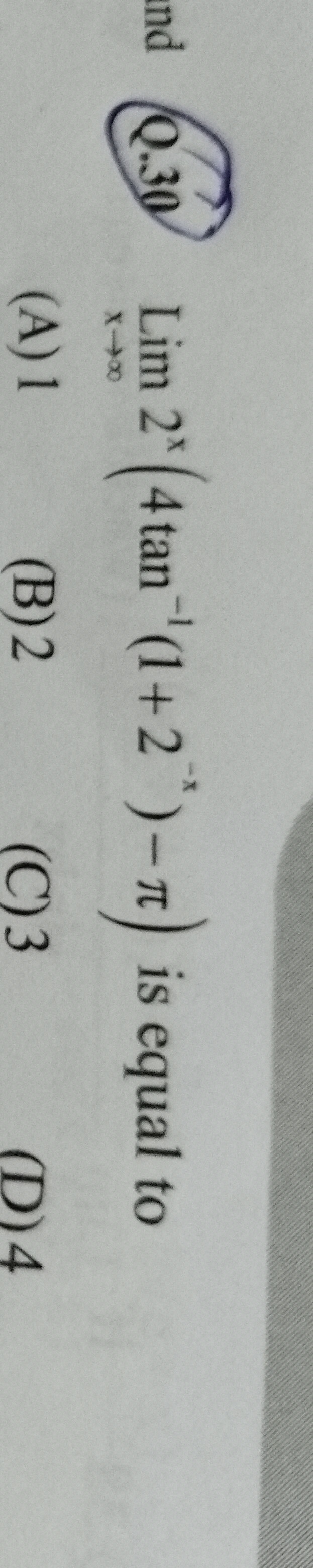
1
2
3
4
2
Solution
Let the given limit be L.
L=limx→∞2x(4tan−1(1+2−x)−π)
Let y=2−x. As x→∞, 2−x→0, so y→0. Also, 2x=2−x1=y1.
Substituting y into the limit expression, we get:
L=limy→0y1(4tan−1(1+y)−π)
L=limy→0y4tan−1(1+y)−π
As y→0, the numerator approaches 4tan−1(1+0)−π=4tan−1(1)−π=4(4π)−π=π−π=0. The denominator approaches 0.
Thus, the limit is of the indeterminate form 00. We can apply L'Hopital's Rule.
Differentiate the numerator and the denominator with respect to y:
Derivative of the numerator: dyd(4tan−1(1+y)−π)=4⋅1+(1+y)21⋅dyd(1+y)=1+(1+y)24.
Derivative of the denominator: dyd(y)=1.
Applying L'Hopital's Rule:
L=limy→011+(1+y)24=limy→01+(1+y)24
Now, substitute y=0 into the expression:
L=1+(1+0)24=1+124=1+14=24=2
Thus, the value of the limit is 2.
Alternatively, using Taylor series expansion for tan−1(1+y) around y=0:
Let f(y)=tan−1(1+y).
f(0)=tan−1(1)=4π.
f′(y)=1+(1+y)21, so f′(0)=1+(1+0)21=21.
The Taylor expansion of f(y) around y=0 is f(y)=f(0)+f′(0)y+O(y2)=4π+21y+O(y2).
Substitute this into the limit expression:
L=limy→0y4(4π+21y+O(y2))−π
L=limy→0yπ+2y+O(y2)−π
L=limy→0y2y+O(y2)
L=limy→0(2+yO(y2))
L=limy→0(2+O(y))
As y→0, O(y)→0.
L=2
Both methods yield the same result.
