Question
Question: Like that image what is the rule for \(\dfrac{d}{{dx}}(uv)\)? ?
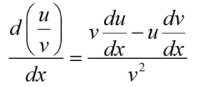
Solution
Let us assume u(x) and v(x) are two differentiable function of x and f(x)=u(x)v(x) and then apply the definition of derivative of f(x),
f′(x)=h→0limhf(x+h)−f(x)
Complete step by step answer:
As, f(x)=u(x)v(x)
Then, f(x+h)=u(x+h)v(x+h)
From the definition of derivative of f(x) we get, f′(x)=h→0limhf(x+h)−f(x) ⇒f′(x)=h→0limhu(x+h)v(x+h)−u(x)v(x) ⇒f′(x)=h→0lim[hu(x+h)v(x+h)−u(x+h)v(x)+hu(x+h)v(x)−u(x)v(x)] ⇒f′(x)=h→0lim[u(x+h)hv(x+h)−v(x)]+h→0lim[v(x)hu(x+h)−u(x)] ⇒f′(x)=u(x)h→0lim[hv(x+h)−v(x)]+h→0v(x)lim[hu(x+h)−u(x)] ∴f′(x)=u(x)v′(x)+v(x)u′(x) i.e.,dxd[u(x)v(x)]=udxdv+vdxdu
Note: It is true for more than two differentiable functions. If a finite number of functions u, v, w, …….. are differentiable with respect to x, then
dxd(uvw...)=(vw...)dxdu+(uw...)dxdv+(uv...)dxdw+...
