Question
Question: Light incident normally on a pane mirror attached to a galvanometer coil retraces backwards as shown...
Light incident normally on a pane mirror attached to a galvanometer coil retraces backwards as shown in Fig. A current in the coil produces a deflection of 3.50 of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5m away?
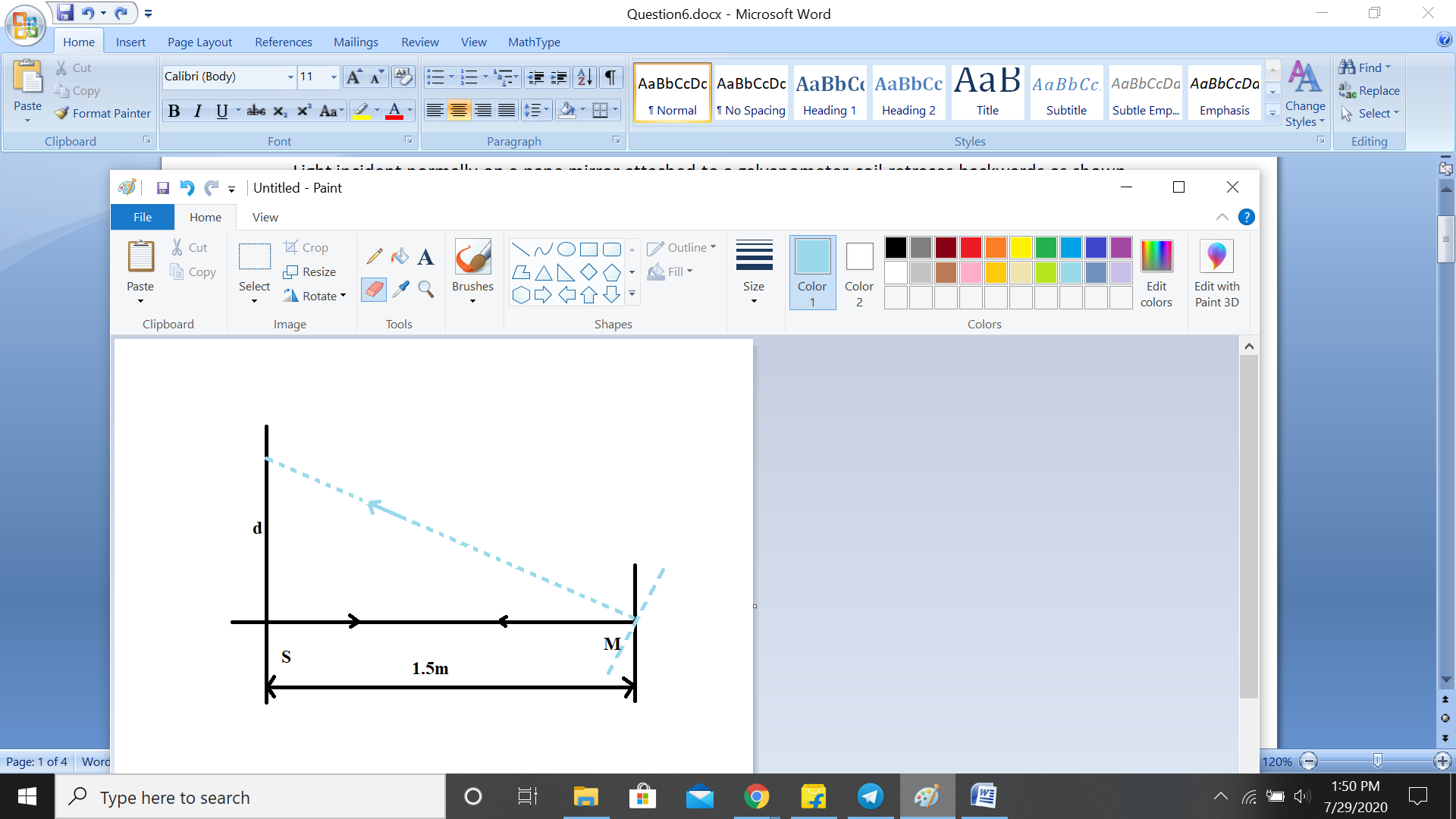
Solution
Hint: When the angle of deflection of incident light is given, we can find the angle of deflection of the reflected rays by doubling the deflection of the incident light. To find the displacement of reflected spot on the screen, we can use the direct formula i.e. tan2θ=1.5d , where θ is the deflection of incident light, d is the displacement of the reflected spot on the screen.
Complete step-by-step solution -
Since the reflected rays get defected by an angle 2θ , here deflection due to incident light i.e. θ is given as 3.50. therefore, we will first calculate the value of 2θ, and then put it in the formula to calculate the displacement.
Computing 2θ, we get
⇒2θ=2×3.50 ⇒2θ=70
Now using the direct formula i.e.tan2θ=1.5d, and substituting the value of 2θ, we get
⇒tan(70)=1.5d ⇒0.123=1.5d ⇒d=0.184m ⇒d=18.4cm
Therefore, the displacement of the reflected spot on light is calculated as 18.4 cm.
Note- The direct formula to calculate the angular deflection should be memorized which is tan2θ=1.5d by which we can also compute displacement for the reflected spot. It is to be noted that θ here in the formula, is in degrees and not radians. So the value of tangent of θ is to be computed carefully. Also to be noted that the reflected rays get deflected by an amount which is twice the angle of deflection by the incident light.
