Question

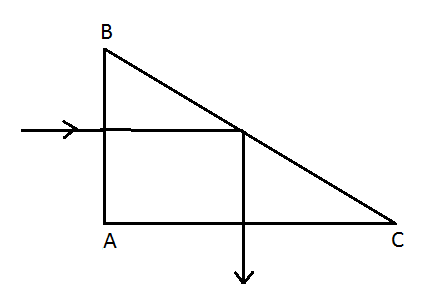
Light enters an isosceles right triangular prism at normal incidence through face AB and undergoes total internal reflection at face BC as shown below. The minimum value of the refractive index of the prism is close to:

A) $1.10$
B) $1.55$
C) $1.42$
D) $1.72$

Answer 1

By using Snell’s Law and knowing the terms of total internal reflection, we have to find the minimum value of the refractive index of the prism.
Total internal reflection: It is defined as the phenomenon which occurs when the ray of light travels from a more optically denser medium to a less optically denser medium. The angle of incidence must be greater than the critical angle. These are the conditions of total internal inflection.
Critical angle: The critical angle occurs when the angle of incidence where the angle of refraction is ${90^ \circ }$.

Formula Used:
We will be using the formula of Snell’s Law i.e., ${n_1}sin{\theta _1} = {n_2}sin{\theta _2}$

Complete step by step solution:
Snell’s Law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, for a given pair of media and for the light of a given color. It gives the relation between the angle of incidence, the angle of refraction and refractive index of a given pair of mediums. It is given by,
${n_1}sin{\theta _1} = {n_2}sin{\theta _2}$
Where,
${n_1}$,${n_2}$are the refractive index of medium $1$ and medium $2$
${\theta _1}$- Angle of incidence
${\theta _2}$- Angle of refraction.
Using Snell’s law,
${n_1}sin{\theta _1} = {n_2}sin{\theta _2}$
Given: From the figure, ${n_1} = 1;{n_2} = ?;{\theta _1} = {90^ \circ };{\theta _2} = {45^ \circ }$

${n_2} = \dfrac{{sin{{90}^ \circ }}}{{\sin {{45}^ \circ }}}$
${n_2} = 1.414$
Hence the minimum value of the refractive index of the prism is close to $1.42$.
The answer is Option $(C)$, $1.42$.

Note: Snell’s law is derived from Fermat’s principle. It states that ‘’light travels in the shortest path that takes the least time’’. Snell’s Law gives the degree of refraction. The law was discovered by Dutch astronomer and Mathematician Willebrord Snell in $1621$.