Question

Lift is accelerated with an acceleration ‘a’. A man in the lift throws the ball upwards with acceleration ${a_0}\left( {{a_0} < a} \right)$ . then the acceleration of the ball observed by the observer standing on earth is:
(A) $\left( {{a_0} + a} \right){\text{ }}upwards$
(B) $\left( {a - {a_0}} \right){\text{ }}downwards$
(C) $\left( {{a_0} + a} \right){\text{ }}downwards$
(D) $\left( {a - {a_0}} \right){\text{ }}upwards$

Answer 1

We will start solving this question by first calculating the force in the whole process. For calculating this force we will make a free body diagram (fbd) and using the diagram we will estimate the force value. Then we will find the acceleration with the man standing on earth as a point of reference.

Complete answer:
Look at the following free body diagram:

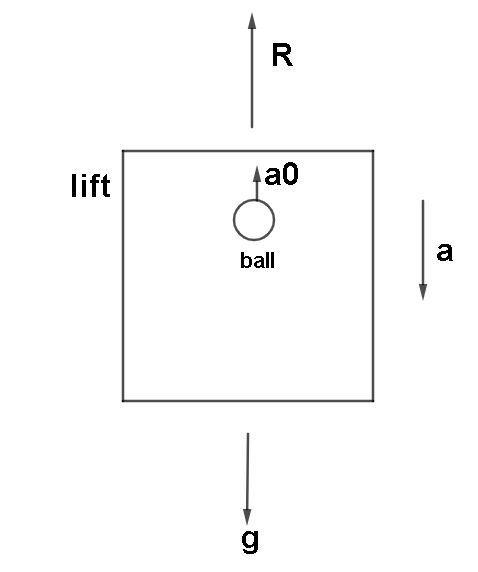
Here g>a where acceleration of the lift g is acceleration due to gravity.
$a_0$ < a where $a_0$ is acceleration of the ball.
Here in the diagram R- force.
Looking at the diagram we get :
$R = mg - ma$
Because g>a.
$R = m\left( {g - a} \right)$ . This will be the force of lift.
Now the observer is on the ground . The acceleration of the ball will be acceleration of lift – acceleration of ball. For the observer standing on the ground the lift is moving at all times, even if the ball is thrown up the observer will see a net downward movement . Hence acceleration of the ball in the lift as observed by man on ground is :
${a_{bm}} = {a_{lm}} - {a_{bl}}$
where,
${a_{bm}}$ = acceleration of the ball with respect to man.
${a_{lm}}$ = acceleration of lift with respect to man
${a_{bl}}$ = acceleration of ball with respect to lift,
${a_{bm}} = a - {a_0}$
And the net acceleration will be downward as observed by man on ground.
Hence the correct answer to this question is option B.

Note:
You can solve this question by eliminating the options. Once you find that the net acceleration is downwards, we can eliminate options A and D. We are left with options B and C. Then only need to find is net acceleration $a - {a_0}$ .