Solveeit Logo
Login

Question

Question: Let $z_1$ be a complex number with $|z_1|=1$ and $z_2$ be any complex number, then $\left|\frac{z_1-...

Let z1z_1 be a complex number with ∣z1∣=1|z_1|=1 and z2z_2 be any complex number, then ∣z1−z21−z1z2‾∣=\left|\frac{z_1-z_2}{1-z_1\overline{z_2}}\right|=

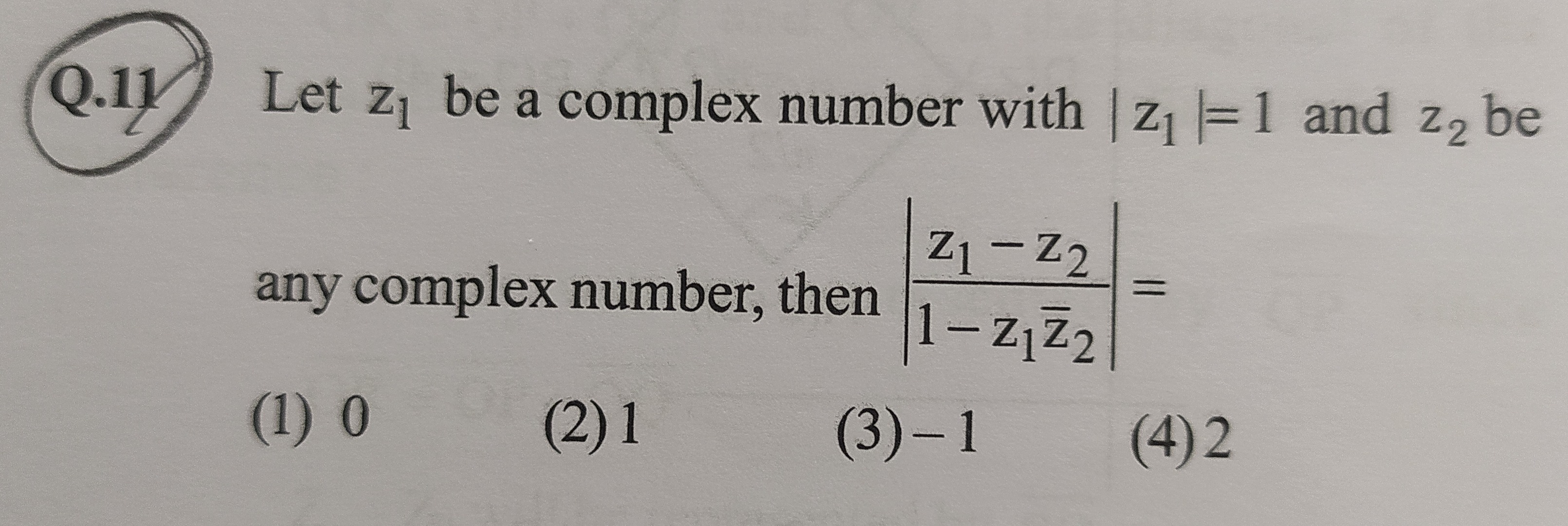
A

0

B

1

C

-1

D

2

Answer

1

Explanation

Solution

Given ∣z1∣=1|z_1| = 1, we need to evaluate

T=∣z1−z21−z1z2‾∣T = \left|\frac{z_1 - z_2}{1 - z_1\overline{z_2}}\right|

Step 1: Compute the modulus squared

Compute numerator modulus squared:

∣z1−z2∣2=(z1−z2)(z1‾−z2‾)=∣z1∣2−z1z2‾−z2z1‾+∣z2∣2.|z_1-z_2|^2 = (z_1-z_2)(\overline{z_1}-\overline{z_2}) = |z_1|^2 - z_1\overline{z_2} - z_2\overline{z_1} + |z_2|^2.

Since ∣z1∣2=1|z_1|^2 = 1, this becomes:

1−z1z2‾−z2z1‾+∣z2∣2.1 - z_1\overline{z_2} - z_2\overline{z_1} + |z_2|^2.

Step 2: Compute the denominator modulus squared

Similarly,

∣1−z1z2‾∣2=(1−z1z2‾)(1−z1‾z2)=1−z1z2‾−z1‾z2+∣z1∣2∣z2∣2.|1-z_1\overline{z_2}|^2 = (1-z_1\overline{z_2})(1-\overline{z_1}z_2) = 1 - z_1\overline{z_2} - \overline{z_1}z_2 + |z_1|^2|z_2|^2.

Again, since ∣z1∣2=1|z_1|^2 = 1:

=1−z1z2‾−z1‾z2+∣z2∣2.= 1 - z_1\overline{z_2} - \overline{z_1}z_2 + |z_2|^2.

Step 3: Conclude the modulus

Thus, both numerator and denominator modulus squared are identical:

∣z1−z2∣2=∣1−z1z2‾∣2.|z_1-z_2|^2 = |1-z_1\overline{z_2}|^2.

Taking square roots gives:

∣z1−z21−z1z2‾∣=∣z1−z2∣∣1−z1z2‾∣=1.\left|\frac{z_1-z_2}{1-z_1\overline{z_2}}\right| = \frac{|z_1-z_2|}{|1-z_1\overline{z_2}|} = 1.

Recognize that both the numerator and denominator have equal modulus squared, so their quotient’s modulus is 1.