Question

Let $z = x + iy$ be a complex number where $x$ and $y$ are integers. Then the area of the rectangle whose vertices are the roots of the equation $\bar z{z^3} + z{\bar z^3} = 350$ is
A. 48
B. 32
C. 40
D. 80

Answer 1

Try to take the common terms and apply the formula $\bar zz = z\bar z = {\left| z \right|^2}$ to reduce the given equation. Then substitute the value of $z\& \bar z$ to find the equations in terms of $x\& y$. Solve those obtained equations to get the vertices of the rectangle and then find its equation to get the final answer.

Complete step-by-step answer :
Given that $z = x + iy$ be a complex number where $x$ and $y$ are integers. So, we have $\bar z = x - iy$.
Also given that $\bar z{z^3} + z{\bar z^3} = 350$.
We know that for a complex number $\bar zz = z\bar z = {\left| z \right|^2}$. By using this formula, we have

$$\Rightarrow \left( {\bar zz} \right){z^2} + \left( {z\bar z} \right){z^2} = 350 \\\ \Rightarrow \left( {\bar zz} \right){z^2} + \left( {z\bar z} \right){{\bar z}^2} = 350 \\\ \Rightarrow {\left| z \right|^2}{z^2} + {\left| z \right|^2}{{\bar z}^2} = 350 \\\ \Rightarrow {\left| z \right|^2}\left( {{z^2} + {{\bar z}^2}} \right) = 350 \\\$$

Substituting $z = x + iy$ and $\bar z = x - iy$ we have

$$\Rightarrow {\left| {x + iy} \right|^2}\left[ {{{\left( {x + iy} \right)}^2} + {{\left( {x - iy} \right)}^2}} \right] = 350 \\\ \Rightarrow {\left( {\sqrt {{x^2} + {y^2}} } \right)^2}\left[ {{{\left( {x + iy} \right)}^2} + {{\left( {x - iy} \right)}^2}} \right] = 350\,{\text{ }}\left[ {\because \left| z \right| = \left| {a + ib} \right| = \sqrt {{a^2} + {b^2}} } \right] \\\ \Rightarrow \left( {{x^2} + {y^2}} \right)\left[ {\left( {{x^2} + 2xiy + {i^2}{y^2}} \right) + \left( {x - 2xiy + {i^2}{y^2}} \right)} \right] = 350 \\\ \Rightarrow \left( {{x^2} + {y^2}} \right)\left( {{x^2} + {x^2} + 2xiy - 2xiy - {y^2} - {y^2}} \right) = 350{\text{ }}\left[ {\because {i^2} = - 1} \right] \\\ \Rightarrow \left( {{x^2} + {y^2}} \right)\left( {2{x^2} - 2{y^2}} \right) = 350 \\\ \Rightarrow \left( {{x^2} + {y^2}} \right)\left( {{x^2} - {y^2}} \right)2 = 350 \\\ \Rightarrow \left( {{x^2} + {y^2}} \right)\left( {{x^2} - {y^2}} \right) = \dfrac{{350}}{2} = 175 \\\$$

Since, $x$ and $y$ are integers we can have two possible ways.
$\left( {{x^2} + {y^2}} \right) = 25\& \left( {{x^2} - {y^2}} \right) = 7$ or $\left( {{x^2} + {y^2}} \right) = 35\& \left( {{x^2} - {y^2}} \right) = 5$
Now consider, $\left( {{x^2} + {y^2}} \right) = 25\& \left( {{x^2} - {y^2}} \right) = 7$. Adding both the equations, we have

$$\Rightarrow \left( {{x^2} + {y^2}} \right) + \left( {{x^2} - {y^2}} \right) = 25 + 7 \\\ \Rightarrow {x^2} + {x^2} + {y^2} - {y^2} = 32 \\\ \Rightarrow 2{x^2} = 32 \\\ \Rightarrow {x^2} = \dfrac{{32}}{2} = 16 \\\ \therefore x = \sqrt {16} = \pm 4...............\left( 1 \right) \\\$$

Subtracting the equation ${x^2} - {y^2} = 7$ from ${x^2} + {y^2} = 25$, we get

$$\Rightarrow \left( {{x^2} + {y^2}} \right) - \left( {{x^2} - {y^2}} \right) = 25 - 7 \\\ \Rightarrow {x^2} - {x^2} + {y^2} + {y^2} = 16 \\\ \Rightarrow 2{y^2} = 18 \\\ \Rightarrow {y^2} = \dfrac{{18}}{2} = 9 \\\ \therefore y = \sqrt 9 = \pm 3 \\\$$

Now, $\left( {{x^2} + {y^2}} \right) = 35\& \left( {{x^2} - {y^2}} \right) = 5$. Adding both the equations, we have

$$\Rightarrow \left( {{x^2} + {y^2}} \right) + \left( {{x^2} - {y^2}} \right) = 35 + 5 \\\ \Rightarrow {x^2} + {x^2} + {y^2} - {y^2} = 40 \\\ \Rightarrow 2{x^2} = 40 \\\ \Rightarrow {x^2} = \dfrac{{40}}{2} = 20 \\\ \therefore x = \sqrt {20} \\\$$

So, for the equations $\left( {{x^2} + {y^2}} \right) = 35\& \left( {{x^2} - {y^2}} \right) = 5$ we are not getting the values of $x$ and $y$ as integers.
Therefore, the vertices of the rectangle are $\left( {x,y} \right) = \left( {4,3} \right),\left( { - 4,3} \right),\left( { - 4, - 3} \right),\left( {4, - 3} \right)$. Let $l$ be the length and $b$ be the width of the rectangle as shown in the figure.

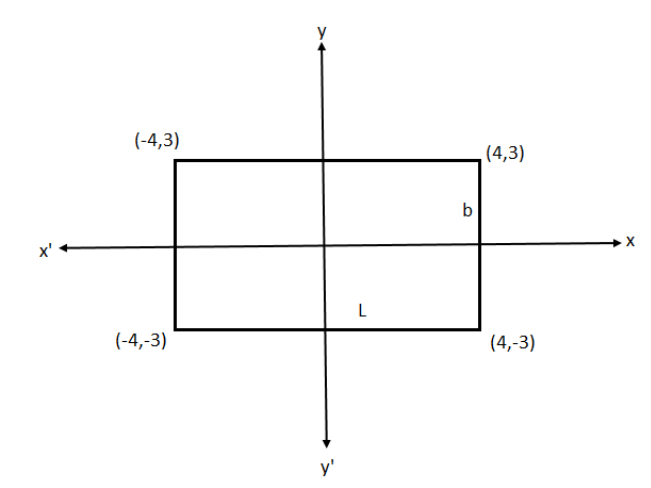
So, $l$ is the distance between the points $\left( {4,3} \right),\left( { - 4,3} \right)$.
Hence $l = \sqrt {{{\left( { - 4 - 4} \right)}^2} + {{\left( {3 - 3} \right)}^2}} = \sqrt {{{\left( { - 8} \right)}^2} + {{\left( 0 \right)}^2}} = 8$
And $b$ is the distance between the points $\left( {4,3} \right),\left( {4, - 3} \right)$
Hence $b = \sqrt {{{\left( {4 - 4} \right)}^2} + {{\left( { - 3 - 3} \right)}^2}} = \sqrt {{{\left( 0 \right)}^2} + {{\left( { - 6} \right)}^2}} = \sqrt {{6^2}} = 6$
We know that if $l\& b$ are length and breadth of rectangle respectively then its area is given by $l \times b$
So, the area of the rectangle formed is equal to $8 \times 6 = 48$.
Thus, the area of the rectangle formed with the vertices is 48 square units.

Note : The distance between the two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$. If $l\& b$ are the length and breadth of the rectangle respectively then its area is given by $l \times b$ square units. Always write the units after the area of the rectangle.