Question

Let $z = \dfrac{{1 + i\sqrt 3 }}{{\sqrt 3 + i}}$ where, $i = \sqrt { - 1}$. Then, in which quadrant ${\bar z^{100}}$ lie?
(a) Fourth quadrant
(b) Third quadrant
(c) Second quadrant
(d) First quadrant

Answer 1

We will be going to use the most curious concept of complex relations to recognize the conjugate by multiplying and dividing the given equation so as to achieve desired value in supposed algebraic equations.

Complete step by step solution:
The condition is related to the complex number as there exists the parameter ‘i’ where the value of instance ‘i’ is $i = \sqrt { - 1}$ respectively.
$\Rightarrow z = \dfrac{{1 + i\sqrt 3 }}{{\sqrt 3 - i}}$
Now, in this case we know that
Multiplying and dividing the complex equation by its conjugate i.e.$\sqrt 3 - i$, we get
$\Rightarrow z = \dfrac{{1 + i\sqrt 3 }}{{\sqrt 3 + i}} \times \dfrac{{\sqrt 3 - i}}{{\sqrt 3 - i}}$
Solving the equation mathematically, we get

$$\Rightarrow z = \dfrac{{\left( {1 + i\sqrt 3 } \right)\left( {\sqrt 3 - i} \right)}}{{\left( {\sqrt 3 + i} \right)\left( {\sqrt 3 - i} \right)}} \\\ \Rightarrow z = \dfrac{{\sqrt 3 - i + 3i - {i^2}\sqrt 3 }}{{3 - {i^2}}} \\\$$

From the complex identity, we know that $i = \sqrt { - 1} \to {i^2} = - 1$
$\Rightarrow z = \dfrac{{\sqrt 3 + 2i + \sqrt 3 }}{{3 + 1}} \\\ \Rightarrow z = \dfrac{{2\sqrt 3 + 2i}}{4} \\\$
Dividing the equation by $2$, we get
$\Rightarrow z = \dfrac{{\sqrt 3 + i}}{2} \\\ \Rightarrow z = \dfrac{{\sqrt 3 }}{2} + i\dfrac{1}{2} \\\$
Hence, the given the equation implies the complex equation $z = a + ib$ where ‘a’ is real and ‘b’ is the imaginary part of the respective equation,
As a result, the above equation can also be written in trigonometric manner in terms of $\sin$ and $\cos$ respectively, we get
$\Rightarrow z = \cos \dfrac{\pi }{6} + i\sin \dfrac{\pi }{6}$
Since, the conjugate for the above equation is,
$\Rightarrow z = \cos \dfrac{\pi }{6} - i\sin \dfrac{\pi }{6}$ respectively
Now, hence we get the solution
$\Rightarrow {{\bar z}^{100}} = {({\text{Conjugate of }}z)^{100}} = \cos 100\dfrac{\pi }{6} - i\sin 100\dfrac{\pi }{6} \\\ \Rightarrow {{\bar z}^{100}} = {({\text{Conjugate of }}z)^{100}} = \cos 50\dfrac{\pi }{3} - i\sin 50\dfrac{\pi }{3} \\\$
Simplifying the equation further, we get
$\Rightarrow {\bar z^{100}} = {({\text{Conjugate of }}z)^{100}} = \cos \dfrac{{2\pi }}{3} - i\sin \dfrac{{2\pi }}{3}$
The equation becomes,
$\Rightarrow {\bar z^{100}} = {({\text{Conjugate of }}z)^{100}} = - \cos \dfrac{{2\pi }}{3} - i\sin \dfrac{{2\pi }}{3}$
Hence, the ${\bar z^{100}}$ lies in III quadrant
$\therefore$The correct option is (b).

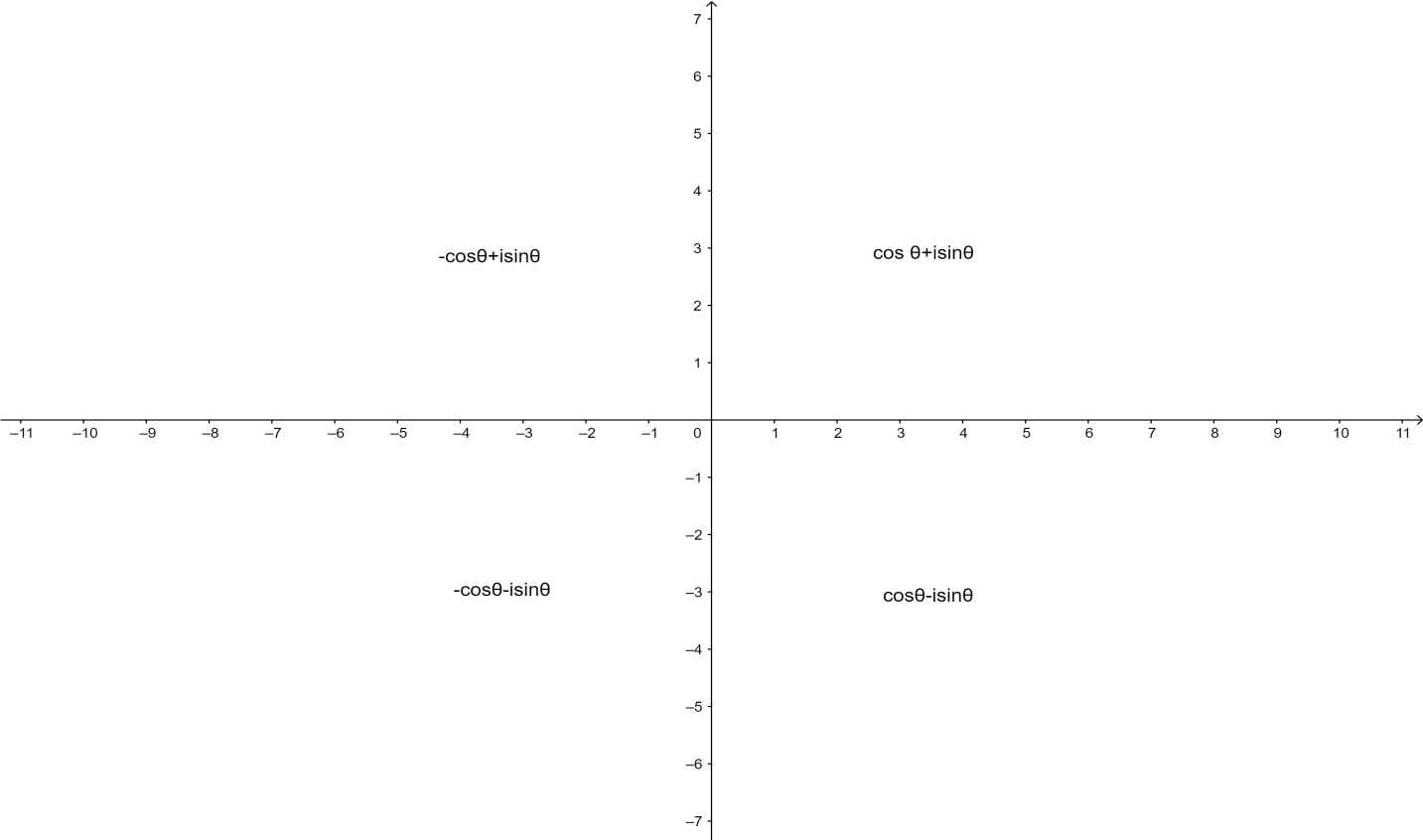
Note:
Considering the basic concept of complex number and its equations say, $z = x + iy$ one must know the analogy behind it where, $x = {\text{real}}$ and $b = {\text{imaginary part}}$, $i = \sqrt { - 1}$. Since, we should also know the conjugate term in algebraic expressions which is just inverse of the term (i.e. sign is opposite such that if +ve implies then it exists –ve conjugate and vice versa). As a result, use the respective formulae and conditions in the calculations to find the desired output (can assume De-Moivre's theorem/equation $z = \cos \theta \pm i\sin \theta$ respectively.