Question

Let${z_1}$, ${z_2}$ be two fixed complex numbers in the argand plane and z be an arbitrary point satisfying$\mid z - {z_1}\mid + \mid z - {z_2}\mid = k$, if$\mid {z_1} - {z_2}\mid < k$, then the locus of z will be represent

Answer 1

Hint : The complex number is a number that consists of two parts in it, one of them is a real number (like 1,2,3, etc.) and the other is an imaginary number which looks like I, 2i, 3i, etc. Those are used in the difficult levels of mathematics where the output cannot be represented normally.
Complete step-by-step answer :
The argand plane represents these complex numbers in its x,y and z axis. (An example for the representation of a complex number is 2+i4).
$\mid z - {z_1}\mid + \mid z - {z_2}\mid = k$ and$\mid {z_1} - {z_2}\mid < k$,
${z_1}$and${z_2}$are the two fixed complex numbers in the argand plane, z being the arbitrary points that satisfy the equation.

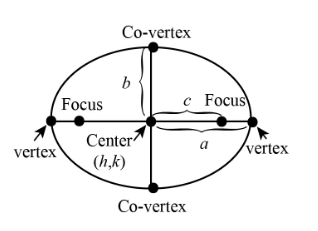
The equation of the ellipse is generally written as$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$. If we write $\dfrac{x}{a} + i\dfrac{y}{b} = z$ and $\dfrac{h}{a} + i\dfrac{k}{b} = {z_1}$, after solving the terms, we will get $\mid z - {z_1}\mid + \mid z - {z_2}\mid = k$, So the given equation when $\mid {z_1} - {z_2}\mid < k$ represents an Ellipse.

Note : The complex numbers are not the normal math types, they are used in the difficult levels, be aware about the formulae of it and try to recognize the equations of the circle, ellipse, parabola, etc in the argand plane, be sure and try to recognize the given equation correctly without any mistake. When there are imaginary values like vector values, then sometimes we won’t get a correct figure as the solution, we need to conclude them by using the denotation small letter i (which means the value is an imaginary or vector value).