Question
Question: Let $y=y(x)$ satisfy the differential equation $(2xy+x^2y+\frac{y^3}{3})dx+(x^2+y^2)dy=0$. If $y(1)=...
Let y=y(x) satisfy the differential equation (2xy+x2y+3y3)dx+(x2+y2)dy=0. If y(1)=1 and the value of (y(0))3=ke(k∈N). Find k.
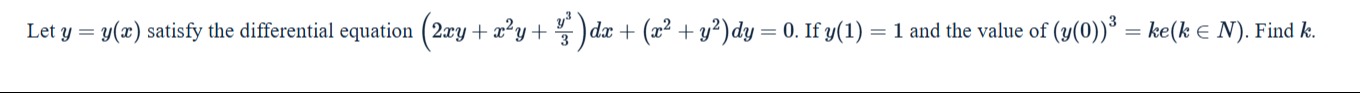
4
Solution
The given differential equation is (2xy+x2y+3y3)dx+(x2+y2)dy=0.
This is a first-order differential equation of the form M(x,y)dx+N(x,y)dy=0, where M(x,y)=2xy+x2y+3y3 and N(x,y)=x2+y2.
First, we check if the equation is exact by comparing the partial derivatives: ∂y∂M=∂y∂(2xy+x2y+3y3)=2x+x2+y2. ∂x∂N=∂x∂(x2+y2)=2x.
Since ∂y∂M=∂x∂N, the equation is not exact.
Next, we look for an integrating factor. Consider the expression N1(∂y∂M−∂x∂N): x2+y21((2x+x2+y2)−2x)=x2+y2x2+y2=1. Since this expression is a function of x only, an integrating factor μ(x) exists and is given by e∫1dx=ex.
Multiply the given differential equation by the integrating factor ex: ex(2xy+x2y+3y3)dx+ex(x2+y2)dy=0. Let the new coefficients be M′(x,y)=ex(2xy+x2y+3y3) and N′(x,y)=ex(x2+y2). We verify that this new equation is exact: ∂y∂M′=∂y∂[ex(2xy+x2y+3y3)]=ex(2x+x2+y2). ∂x∂N′=∂x∂[ex(x2+y2)]=ex(x2+y2)+ex(2x)=ex(x2+2x+y2). Since ∂y∂M′=∂x∂N′, the equation is exact.
Now we find the potential function F(x,y) such that dF=M′dx+N′dy. We have ∂y∂F=N′(x,y)=ex(x2+y2). Integrate with respect to y (treating x as a constant): F(x,y)=∫ex(x2+y2)dy=ex∫(x2+y2)dy=ex(x2y+3y3)+h(x), where h(x) is an arbitrary function of x.
Now, differentiate F(x,y) with respect to x and set it equal to M′(x,y): ∂x∂F=∂x∂[ex(x2y+3y3)+h(x)]=ex(x2y+3y3)+ex(2xy)+h′(x). We are given M′(x,y)=ex(2xy+x2y+3y3). So, ex(x2y+3y3)+ex(2xy)+h′(x)=ex(2xy+x2y+3y3). exx2y+ex3y3+ex2xy+h′(x)=ex2xy+exx2y+ex3y3. This simplifies to h′(x)=0. Integrating with respect to x, we get h(x)=C0, where C0 is a constant.
The general solution is F(x,y)=C1, where C1 is a constant. ex(x2y+3y3)+C0=C1. Let C=C1−C0. The general solution is ex(x2y+3y3)=C.
We are given the initial condition y(1)=1. Substitute x=1 and y=1 into the general solution: e1(12⋅1+313)=C. e(1+31)=C. e(34)=C. C=34e.
The particular solution is ex(x2y+3y3)=34e.
We need to find the value of (y(0))3. Let y0=y(0) be the value of y when x=0. Substitute x=0 into the particular solution: e0(02⋅y0+3y03)=34e. 1(0+3y03)=34e. 3y03=34e. y03=4e.
So, (y(0))3=4e. We are given that (y(0))3=ke, where k∈N. Comparing 4e with ke, we have ke=4e. Since e=0, we can divide by e to get k=4. The value k=4 is a natural number.
