Question
Question: Let $y = y(x)$ be the solution of the differential equation $\frac{dy}{dx} + 2y = f(x)$, where $f(x)...
Let y=y(x) be the solution of the differential equation dxdy+2y=f(x), where f(x)={1,x∈[0,1]0,otherwise
If y(0)=0, then y(23) is:
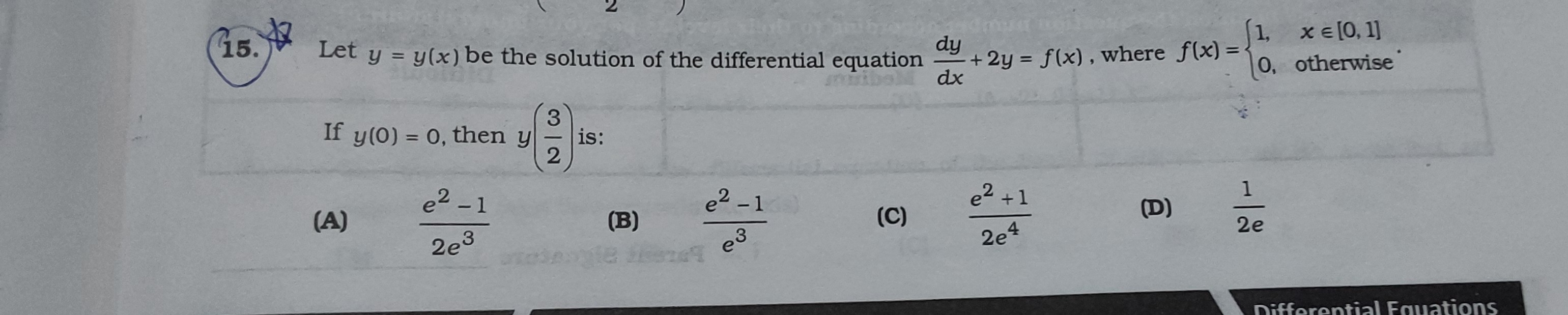
2e3e2−1
e3e2−1
2e4e2+1
2e1
(A) 2e3e2−1
Solution
The given differential equation is a first-order linear differential equation: dxdy+2y=f(x) where f(x) is a piecewise function: f(x)={1,0,x∈[0,1]otherwise The initial condition is y(0)=0. We need to find y(23).
The differential equation is of the form dxdy+P(x)y=Q(x), with P(x)=2. The integrating factor (IF) is e∫P(x)dx=e∫2dx=e2x.
We solve the differential equation in two intervals:
Case 1: x∈[0,1] In this interval, f(x)=1. The differential equation becomes: dxdy+2y=1 Multiplying by the integrating factor e2x: e2xdxdy+2e2xy=e2x The left side is the derivative of (ye2x): dxd(ye2x)=e2x Integrating both sides with respect to x: ye2x=∫e2xdx+C1 ye2x=2e2x+C1 Dividing by e2x to find y(x): y(x)=21+C1e−2x Now, apply the initial condition y(0)=0: 0=21+C1e−2(0) 0=21+C1 C1=−21 So, for x∈[0,1], the solution is: y(x)=21−21e−2x
Case 2: x>1 In this interval, f(x)=0. The differential equation becomes: dxdy+2y=0 Multiplying by the integrating factor e2x: e2xdxdy+2e2xy=0 dxd(ye2x)=0 Integrating both sides with respect to x: ye2x=C2 y(x)=C2e−2x To ensure that y(x) is a continuous solution, the value of y(x) at x=1 must be the same for both expressions. From Case 1, y(1)=21−21e−2(1)=21−21e−2. From Case 2, y(1)=C2e−2(1)=C2e−2. Equating these two values: C2e−2=21−21e−2 C2=(21−21e−2)e2 C2=21e2−21e−2e2 C2=2e2−1 So, for x>1, the solution is: y(x)=(2e2−1)e−2x
Finally, we need to find y(23). Since 23=1.5, which is greater than 1, we use the solution from Case 2: y(23)=(2e2−1)e−2⋅23 y(23)=(2e2−1)e−3 y(23)=2e3e2−1
Comparing this result with the given options: (A) 2e3e2−1 (B) e3e2−1 (C) 2e4e2+1 (D) 2e1
The calculated value matches option (A).
