Question

Let $y = \cos x\left( {\cos x - \cos 3x} \right)$, then $y$ is
A) $\geqslant 0$ only when $x \geqslant 0$
B) $\leqslant 0$ for all real $x \leqslant 0$
C) $\geqslant 0$ for all real $x \geqslant 0$
D) $\leqslant 0$ only when $x \leqslant 0$

Answer 1

In order to solve the equation, first solve the equation inside the parenthesis, by expanding the value of $\cos 3x$ into the formula $\cos 3x = \left( {4{{\cos }^3}x - \cos x} \right)$, then add or subtract the common terms, and if left something common that can be taken out from the bracket and further be solved.

Complete step by step solution:
We are given an equation $y = \cos x\left( {\cos x - \cos 3x} \right)$, in order to solve for $y$, we are expanding or solving the parenthesis.
From the trigonometric identities we know that $\cos 3x = \left( {4{{\cos }^3}x - 3 \cos x} \right)$, so substituting this value in the above equation $y = \cos x\left( {\cos x - \cos 3x} \right)$, we get:
$y = \cos x\left( {\cos x - \left( {4{{\cos }^3}x - 3\cos x} \right)} \right)$
Opening the inner brackets:
$y = \cos x\left( {\cos x - 4{{\cos }^3}x + 3\cos x} \right)$
Adding $3\cos x$ and $\cos x$ inside the bracket and we get:
$y = \cos x\left( {4\cos x - 4{{\cos }^3}x} \right)$
Since, we can see that $4\cos x$ is common in both $4{\cos ^3}x$ and $4\cos x$, so taking the common value outside the bracket, we get:
$y = 4{\cos ^2}x\left( {1 - {{\cos }^2}x} \right)$
From the trigonometric identities, we know that $\left( {1 - {{\cos }^2}x} \right) = {\sin ^2}x$, so replacing $\left( {1 - {{\cos }^2}x} \right)$ from ${\sin ^2}x$ in the bracket of the above equation, and we get:
$y = 4{\cos ^2}x{\sin ^2}x$ which can be written as $y = 4{\cos ^2}x{\sin ^2}x = {\left( {2\cos x\sin x} \right)^2}$
From the trigonometric angles and sub-angles, we also know that $2\cos x\sin x = \sin 2x$, so replacing the above obtained value of $y$ with this identity, we get:
$y = {\left( {2\cos x\sin x} \right)^2} = {\left( {\sin 2x} \right)^2}$
Since, we know that $\sin x$ is always greater than or equal zero for any real number that is greater than or equal to zero. So, from this concept the value of $y \geqslant 0$if for any real number $x \geqslant 0$. And this answer matches with the third option.

Therefore, for $y = \cos x\left( {\cos x - \cos 3x} \right)$, $y$ is $\geqslant 0$ for all real $x \geqslant 0$, which means the option (C) is correct.
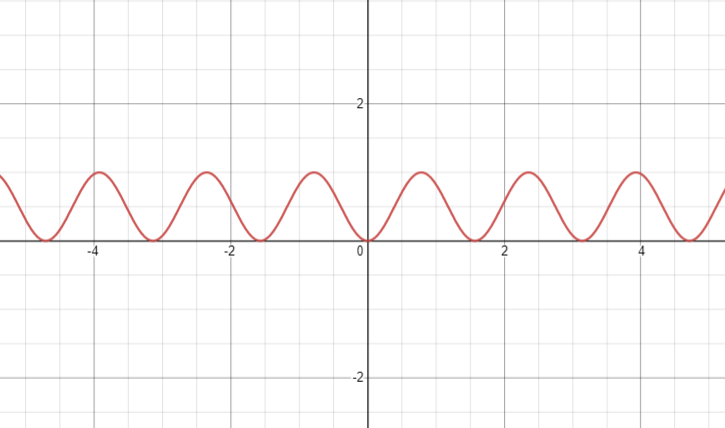
The graph of the given function is as shown below:

Note:

It’s important to remember the trigonometric identities formulas like, $\left( {1 - {{\cos }^2}x} \right) = {\sin ^2}x$ and $\cos 3x = \left( {4{{\cos }^3}x - \cos x} \right)$ to solve this kind of questions.
Do not commit a mistake by taking $\cos x$ common from $\left( {\cos x - \cos 3x} \right)$, as there is nothing common in them, we need to expand it.