Question
Question: Let $y = 2 \tan^{-1}x$ and $z = \sin^{-1} \frac{2x}{1 + x^2}$, then $\left|\frac{dy}{dz}\right|$ equ...
Let y=2tan−1x and z=sin−11+x22x, then dzdy equals
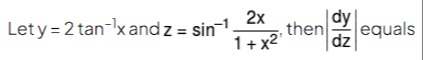
-1
0
1
2
1
Solution
Let y=2tan−1x and z=sin−11+x22x. We want to find dzdy.
We can find dzdy using the chain rule: dzdy=dz/dxdy/dx.
First, find dxdy: y=2tan−1x dxdy=dxd(2tan−1x)=2⋅1+x21=1+x22.
Next, find dxdz: z=sin−11+x22x. Let x=tanθ, where θ=tan−1x. Then 1+x22x=1+tan2θ2tanθ=sin(2θ). So, z=sin−1(sin(2θ))=sin−1(sin(2tan−1x)).
The value of sin−1(sinu) depends on the range of u. sin−1(sinu)=u if u∈[−2π,2π]. sin−1(sinu)=π−u if u∈[2π,23π]. sin−1(sinu)=−π−u if u∈[−23π,−2π]. In our case, u=2tan−1x. The range of tan−1x is (−2π,2π), so the range of 2tan−1x is (−π,π).
We consider different cases for the value of x:
Case 1: −1<x<1. If −1<x<1, then −4π<tan−1x<4π. Then −2π<2tan−1x<2π. In this range, z=sin−1(sin(2tan−1x))=2tan−1x. So, z=y. dxdz=dxd(2tan−1x)=1+x22. Then dzdy=dz/dxdy/dx=2/(1+x2)2/(1+x2)=1.
Case 2: x>1. If x>1, then 4π<tan−1x<2π. Then 2π<2tan−1x<π. In this range, u=2tan−1x∈(2π,π). This range is part of [2π,23π]. z=sin−1(sin(2tan−1x))=π−2tan−1x. So, z=π−y. dxdz=dxd(π−2tan−1x)=0−1+x22=−1+x22. Then dzdy=dz/dxdy/dx=−2/(1+x2)2/(1+x2)=−1.
Case 3: x<−1. If x<−1, then −2π<tan−1x<−4π. Then −π<2tan−1x<−2π. In this range, u=2tan−1x∈(−π,−2π). This range is part of [−23π,−2π]. z=sin−1(sin(2tan−1x))=−π−2tan−1x. So, z=−π−y. dxdz=dxd(−π−2tan−1x)=0−1+x22=−1+x22. Then dzdy=dz/dxdy/dx=−2/(1+x2)2/(1+x2)=−1.
The derivative dxdz is not defined at x=1 and x=−1 because the function z=sin−11+x22x is not differentiable at these points. However, the question asks for dzdy.
If ∣x∣<1, dzdy=1. If ∣x∣>1, dzdy=−1.
In both cases where the derivative exists (x=1,x=−1), the absolute value of dzdy is 1. dzdy=∣1∣=1 if ∣x∣<1. dzdy=∣−1∣=1 if ∣x∣>1.
Thus, for all x where the derivative exists, dzdy=1.
