Question

Let ${{y}^{2}}=4ax$ be a parabola and ${{x}^{2}}+{{y}^{2}}+2bx=0$be a circle. If parabola and circle touch each other externally then:
(a) $a>0,b>0$
(b) $a>0,b<0$
(c) $a<0,b>0$
(d) None of these

Answer 1

Hint: To solve this we will use the concept that if the parabola and circle touch each other then they have a common tangent, given by equation $x-yt+a{{t}^{2}}=0$.

Complete step-by-step answer:

We have been given the equation of the circle in the question as ${{x}^{2}}+{{y}^{2}}+2bx=0$.
We know that the general equation of a circle is given by ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$, where $\left( a,b \right)$ represents the center of the circle and $r$ represents the radius of the circle.
So, to convert the given equation in the general form, we can use the method of completing squares. Now, adding and subtracting ${{b}^{2}}$ we get,
${{x}^{2}}+{{y}^{2}}+2bx+{{b}^{2}}-{{b}^{2}}=0$
Clubbing terms together, we get
$\left( {{x}^{2}}+2bx+{{b}^{2}} \right)+{{y}^{2}}={{b}^{2}}$
Since we know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$, we can write
${{\left( x+b \right)}^{2}}+{{y}^{2}}={{b}^{2}}$
Thus, comparing with the general equation of the circle, we get the center of the circle as $\left( -b,0 \right)$ and the radius as $b$.
We can plot a rough graph of the circle and the parabola given in the question. As we can see from the plot given below, the circle and parabola touch each other externally. Hence, they will have a common tangent.
To find the equation of the tangent to the parabola, we have to consider a point $P$ on the parabola having coordinates as $\left( a{{t}^{2}},2at \right)$, as in the figure.

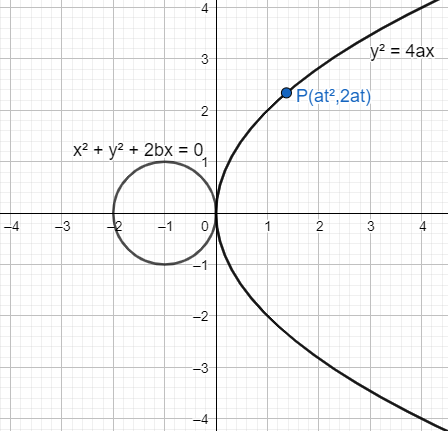
We have to consider the equation of the parabola, i.e. ${{y}^{2}}=4ax$and differentiate it with respect to $x$ to get the slope of the tangent. So, we get
$\begin{aligned} & 2y\dfrac{dy}{dx}=4a \\\ & \dfrac{dy}{dx}=\dfrac{4a}{2y} \\\ & \dfrac{dy}{dx}=\dfrac{2a}{y} \\\ \end{aligned}$
Since point $P$ lies on the parabola, we can substitute $x=a{{t}^{2}},y=2at$in the above equation. So, we get

& \dfrac{dy}{dx}=\dfrac{2a}{2at} \\\ & \dfrac{dy}{dx}=\dfrac{1}{t} \\\ \end{aligned}$$ $\dfrac{dy}{dx}=\dfrac{2a}{2at}$ $\dfrac{dy}{dx}=\dfrac{1}{t}$ So, therefore, we have obtained the slope of the tangent as $$\dfrac{1}{t}$$. We know that the equation of a line through point $\left( {{x}_{1}},{{y}_{1}} \right)$ and slope $$m$$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. We can obtain the equation of tangent by substituting the point as $\left( a{{t}^{2}},2at \right)$ and slope as $$\dfrac{1}{t}$$ in the general equation of line. Therefore, we get the equation of the tangent as, $$y-2at=\dfrac{1}{t}\left( x-a{{t}^{2}} \right)$$ On rearranging we get, $$\begin{aligned} & yt-2a{{t}^{2}}=x-a{{t}^{2}} \\\ & x-yt+a{{t}^{2}}=0 \\\ \end{aligned}$$ Now we know that the perpendicular distance from the center of the circle $$\left( -b,0 \right)$$ to the tangent $$x-yt+a{{t}^{2}}=0$$ is the radius, which we know is $b$. The formula to find shortest distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and a line $$ax+by+c=0$$ is $$\dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$. So, we can relate the perpendicular distance from the center $$\left( -b,0 \right)$$ and tangent $$x-yt+a{{t}^{2}}=0$$ to the radius as $$\begin{aligned} & \dfrac{\left( 1\times -b \right)+\left( -t\times 0 \right)+a{{t}^{2}}}{\sqrt{{{1}^{2}}+{{\left( -t \right)}^{2}}}}=b \\\ & \dfrac{-b+0+a{{t}^{2}}}{\sqrt{1+{{t}^{2}}}}=b \\\ & \dfrac{a{{t}^{2}}-b}{\sqrt{1+{{t}^{2}}}}=b \\\ \end{aligned}$$ Squaring both sides, we get $$\begin{aligned} & {{\left[ \dfrac{a{{t}^{2}}-b}{\sqrt{1+{{t}^{2}}}} \right]}^{2}}={{b}^{2}} \\\ & \dfrac{{{\left( a{{t}^{2}}-b \right)}^{2}}}{1+{{t}^{2}}}={{b}^{2}} \\\ & {{\left( a{{t}^{2}}-b \right)}^{2}}={{b}^{2}}\left( 1+{{t}^{2}} \right) \\\ \end{aligned}$$ Since we know that $${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$$, we can expand as, $${{a}^{2}}{{t}^{4}}-2ab{{t}^{2}}+{{b}^{2}}={{b}^{2}}+{{b}^{2}}{{t}^{2}}$$ Cancelling out similar terms, we get $$\begin{aligned} & {{a}^{2}}{{t}^{4}}-2ab{{t}^{2}}={{b}^{2}}{{t}^{2}} \\\ & {{a}^{2}}{{t}^{4}}=2ab{{t}^{2}}+{{b}^{2}}{{t}^{2}} \\\ \end{aligned}$$ Taking out common terms from the RHS, we get $${{a}^{2}}{{t}^{4}}=b{{t}^{2}}\left( 2a+b \right)$$ Cancelling out $${{t}^{2}}$$, we get $$\begin{aligned} & {{a}^{2}}{{t}^{2}}=b\left( 2a+b \right) \\\ & {{t}^{2}}=\dfrac{b\left( 2a+b \right)}{{{a}^{2}}} \\\ \end{aligned}$$ We know that $${{t}^{2}}\ge 0$$, therefore, we can write that $$\dfrac{b\left( 2a+b \right)}{{{a}^{2}}}\ge 0$$. We know that $${{a}^{2}}\ge 0$$ as square is always positive, and so we get that the denominator is always positive. The term $$\dfrac{b\left( 2a+b \right)}{{{a}^{2}}}\ge 0$$ is valid when both numerator and denominator are either positive or negative. So, we get the result that the numerator is also positive, which means that $b\left( 2a+b \right)\ge 0$. So, again two cases can arise, either $$b$$ and $$\left( 2a+b \right)$$ are both positive or negative, for the condition to be true. Let us consider the first case, when both are positive. So, we get that $b\ge 0$ or $$2a+b\ge 0$$. Now, since we know that $b\ge 0$, for $$2a+b\ge 0$$ to hold true, $$a\ge 0$$. Therefore, one condition that we have obtained is that $$a>0,b>0$$. Let us consider the second case, when both are negative. So, we get that $b\le 0$ or $$2a+b\le 0$$. Now, since we know that $b\le 0$, for $$2a+b\le 0$$ to hold true, $$a\le 0$$. Therefore, the next condition that we have obtained is that $$a<0,b<0$$. So, we can conclude that both $$a$$ and $$b$$ must have the same signs. Either both are positive or both are negative. Looking at the options, we get that option (a) is the correct answer. Note: After reading the question, you must be able to plot a graph and see that the circle and parabola share the same tangent, only then you can frame the solution. You can avoid computing the equation of the tangent if you memorise $$yt=x+a{{t}^{2}}$$, which is very useful in solving such questions.