Question

Let $(x^2 + 2x + 2)^{20} = a_0 + a_1x + a_2x^2 + \dots + a_{40}x^{40}$, then the value of $(20a_0 - a_1 + a_{39})$ is equal to

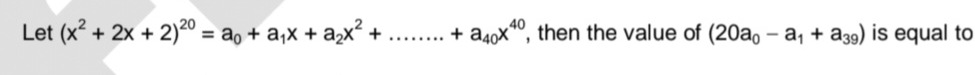
• A. 0
• B. 40
• C. $2^{20}$
• D. $20 \cdot 2^{20}$

Answer 1

Answer: (B)

40

Answer 2

Let $P(x) = (x^2 + 2x + 2)^{20} = a_0 + a_1x + a_2x^2 + \dots + a_{40}x^{40}$.

To find $a_0$, we set $x=0$: $a_0 = P(0) = (0^2 + 2(0) + 2)^{20} = 2^{20}$.

To find $a_1$, we need the first derivative of $P(x)$: $P'(x) = \frac{d}{dx}(x^2 + 2x + 2)^{20} = 20(x^2 + 2x + 2)^{19}(2x + 2)$. Setting $x=0$: $a_1 = P'(0) = 20(0^2 + 2(0) + 2)^{19}(2(0) + 2) = 20(2^{19})(2) = 20 \cdot 2^{20}$.

Now, consider the term $20a_0 - a_1$: $20a_0 - a_1 = 20(2^{20}) - (20 \cdot 2^{20}) = 0$.

So, the expression simplifies to $0 + a_{39} = a_{39}$.

To find $a_{39}$, we use the property of reciprocal polynomials. Let $R(x) = x^{40}P(1/x)$. $R(x) = x^{40} \left(\left(\frac{1}{x}\right)^2 + 2\left(\frac{1}{x}\right) + 2\right)^{20}$ $R(x) = x^{40} \left(\frac{1 + 2x + 2x^2}{x^2}\right)^{20}$ $R(x) = x^{40} \frac{(2x^2 + 2x + 1)^{20}}{x^{40}}$ $R(x) = (2x^2 + 2x + 1)^{20}$.

The expansion of $x^{40}P(1/x)$ is $x^{40}(a_0 + a_1/x + a_2/x^2 + \dots + a_{40}/x^{40}) = a_0x^{40} + a_1x^{39} + a_2x^{38} + \dots + a_{40}$. Comparing the coefficients of $R(x)$ with $a_0x^{40} + a_1x^{39} + \dots + a_{40}$, we see that the coefficient of $x^{39}$ in $P(x)$ ($a_{39}$) is the coefficient of $x^1$ in $R(x)$.

Let $R(x) = b_0 + b_1x + b_2x^2 + \dots + b_{40}x^{40}$. Then $a_{39} = b_1$. To find $b_1$, we can differentiate $R(x)$: $R'(x) = \frac{d}{dx}(2x^2 + 2x + 1)^{20} = 20(2x^2 + 2x + 1)^{19}(4x + 2)$. Setting $x=0$: $b_1 = R'(0) = 20(2(0)^2 + 2(0) + 1)^{19}(4(0) + 2) = 20(1)^{19}(2) = 40$.

Therefore, $a_{39} = 40$.

The value of the expression $(20a_0 - a_1 + a_{39})$ is $0 + 40 = 40$.