Question
Question: Let $x<1$, then value of $\begin{vmatrix} x^2+2 & 2x+1 & 2log_4 2 \\ 2x+1 & x+2 & 2log_9 3 \\ log_2 ...
Let x<1, then value of x2+22x+1log282x+1x+2log3272log422log932log164
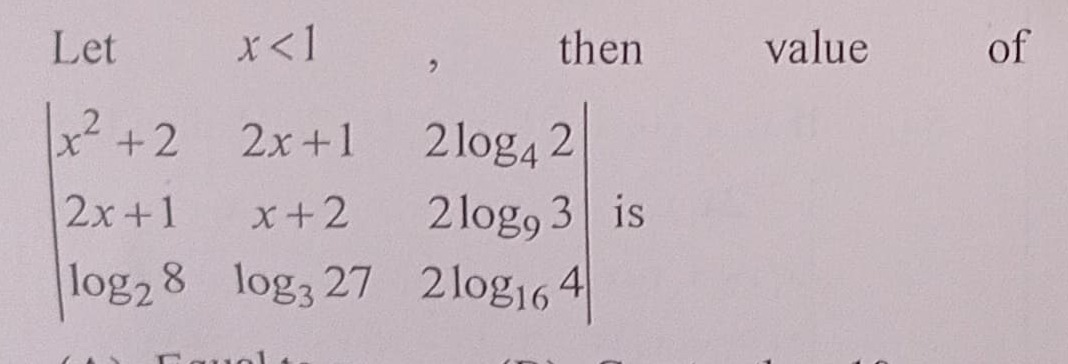
(x−1)2(x−3)
Solution
To evaluate the given determinant, we first simplify the logarithmic terms.
The determinant is: D=x2+22x+1log282x+1x+2log3272log422log932log164
Let's simplify each logarithmic term:
-
2log42=log4(22)=log44=1 (Alternatively, using change of base formula: 2×log24log22=2×21=1)
-
2log93=log9(32)=log99=1 (Alternatively: 2×log39log33=2×21=1)
-
log28=log2(23)=3
-
log327=log3(33)=3
-
2log164=log16(42)=log1616=1 (Alternatively: 2×log416log44=2×21=1)
Substitute these simplified values back into the determinant: D=x2+22x+132x+1x+23111
Now, we can simplify the determinant using row operations. Apply the operations R1→R1−R3 and R2→R2−R3:
For R1: (x2+2)−3=x2−1 (2x+1)−3=2x−2 1−1=0
For R2: (2x+1)−3=2x−2 (x+2)−3=x−1 1−1=0
The determinant becomes: D=x2−12x−232x−2x−13001
Expand the determinant along the third column (C3): D=0⋅(cofactor of (1,3))−0⋅(cofactor of (2,3))+1⋅x2−12x−22x−2x−1 D=1⋅[(x2−1)(x−1)−(2x−2)(2x−2)]
Factor out common terms: x2−1=(x−1)(x+1) 2x−2=2(x−1)
Substitute these into the expression for D: D=(x−1)(x+1)(x−1)−[2(x−1)][2(x−1)] D=(x−1)2(x+1)−4(x−1)2
Now, factor out (x−1)2: D=(x−1)2[(x+1)−4] D=(x−1)2(x−3)
The given condition x<1 does not further simplify the expression, it just specifies the domain for x.
The final answer is (x−1)2(x−3).
Explanation of the solution:
-
Simplify all logarithmic terms in the determinant using logarithm properties.
-
Substitute the numerical values of the simplified logarithmic terms back into the determinant.
-
Apply row operations (R1→R1−R3 and R2→R2−R3) to create zeros in the third column, simplifying the expansion.
-
Expand the determinant along the third column.
-
Factorize the terms in the resulting 2×2 determinant and simplify the expression to obtain the final value.
