Question
Question: Let $(x, y, z)$ be an ordered triplet of real numbers, such that $x < 1, y < 2, z < 3$ and $x + \fra...
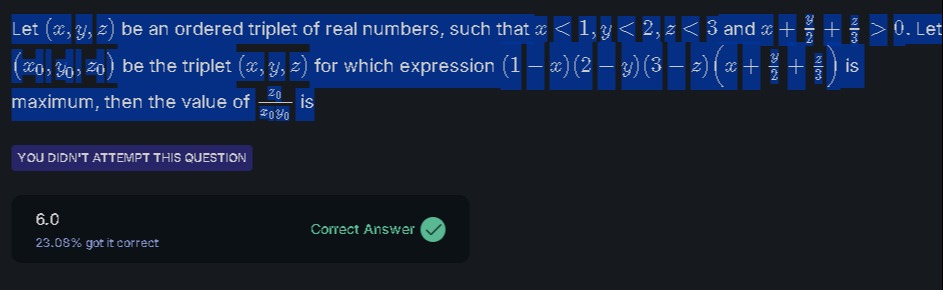
Let (x,y,z) be an ordered triplet of real numbers, such that x<1,y<2,z<3 and x+2y+3z>0. Let (x0,y0,z0) be the triplet (x,y,z) for which expression (1−x)(2−y)(3−z)(x+2y+3z) is maximum, then the value of x0y0z0 is
0
6
Solution
To maximize the expression P=(1−x)(2−y)(3−z)(x+2y+3z) under the given constraints, we use the AM-GM inequality.
1. Introduce new variables: Let a=1−x, b=2−y, c=3−z. From the constraints x<1,y<2,z<3, we have a>0,b>0,c>0.
2. Express x,y,z in terms of a,b,c: x=1−a y=2−b z=3−c
3. Substitute into the expression: The expression becomes P=a⋅b⋅c⋅((1−a)+22−b+33−c). Simplify the last term: x+2y+3z=(1−a)+(1−2b)+(1−3c)=3−a−2b−3c. Let d=3−a−2b−3c. The constraint x+2y+3z>0 means d>0. So, the expression to maximize is P=a⋅b⋅c⋅d.
4. Apply AM-GM inequality: To apply AM-GM effectively, we need a product of terms whose sum is constant. Consider the following four positive terms: u1=a u2=2b u3=3c u4=3−a−2b−3c
The sum of these terms is: u1+u2+u3+u4=a+2b+3c+(3−a−2b−3c)=3. This sum is a constant.
Now, express P in terms of u1,u2,u3,u4: a=u1 b=2u2 c=3u3 P=u1⋅(2u2)⋅(3u3)⋅u4=6⋅u1u2u3u4.
By the AM-GM inequality, for non-negative numbers u1,u2,u3,u4: 4u1+u2+u3+u4≥4u1u2u3u4 Substituting the sum: 43≥4u1u2u3u4 Raising both sides to the power of 4: (43)4≥u1u2u3u4 u1u2u3u4≤25681.
The maximum value of u1u2u3u4 is 25681. The maximum value of P is 6⋅25681=128243.
5. Find the values of x0,y0,z0 for which the maximum occurs: The equality in AM-GM holds when all terms are equal: u1=u2=u3=u4. Since their sum is 3, each term must be 43. u1=a=43 u2=2b=43⟹b=46=23 u3=3c=43⟹c=49 And u4=3−a−2b−3c=3−43−43−43=3−49=43, which is consistent.
Now, find x0,y0,z0: x0=1−a=1−43=41 y0=2−b=2−23=21 z0=3−c=3−49=43
6. Calculate the required expression: We need to find the value of x0y0z0. x0y0z0=(1/4)(1/2)3/4=1/83/4 x0y0z0=43×8=3×2=6.
The final answer is 6.
