Question

Let x, y, z are real numbers such that xyz + x + z = y and xz ≠ 1. If the greatest value of the expression $(\frac{2}{1+x^2} - \frac{2}{1+y^2} + \frac{3}{1+z^2})$ is $\frac{p}{q}$, where p and q are relatively prime, then (p - q) is equal to

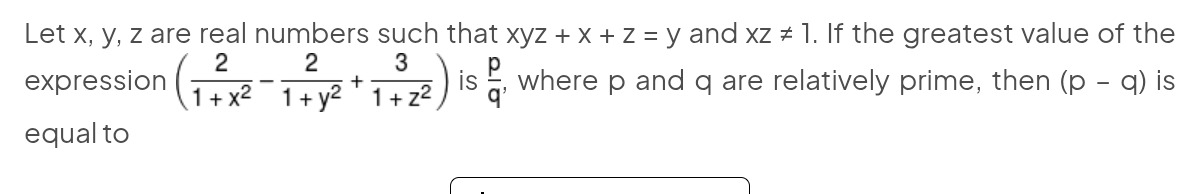
• A. 2
• B. 3
• C. 1
• D. 4

Answer 1

Answer: (A)

2

Answer 2

Given the equation $xyz + x + z = y$, we can rearrange it to $y(1-xz) = x+z$. Since $xz \neq 1$, we can write $y = \frac{x+z}{1-xz}$.

This expression for $y$ is reminiscent of the tangent addition formula: $\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}$. Let $x = \tan \alpha$ and $z = \tan \beta$. Then $y = \tan(\alpha + \beta)$. The condition $xz \neq 1$ ensures that $\tan \alpha \tan \beta \neq 1$, which means $\alpha + \beta \neq \frac{\pi}{2} + k\pi$ for any integer $k$, ensuring $\tan(\alpha+\beta)$ is well-defined.

The expression to maximize is $E = \frac{2}{1+x^2} - \frac{2}{1+y^2} + \frac{3}{1+z^2}$. Using the identity $1+\tan^2 \theta = \sec^2 \theta$, we have $\frac{1}{1+\tan^2 \theta} = \cos^2 \theta$. Substituting $x = \tan \alpha$, $y = \tan(\alpha + \beta)$, and $z = \tan \beta$: $E = 2 \cos^2 \alpha - 2 \cos^2(\alpha + \beta) + 3 \cos^2 \beta$.

Using the identity $\cos^2 \theta = \frac{1 + \cos(2\theta)}{2}$: $E = 2 \left(\frac{1 + \cos(2\alpha)}{2}\right) - 2 \left(\frac{1 + \cos(2(\alpha + \beta))}{2}\right) + 3 \left(\frac{1 + \cos(2\beta)}{2}\right)$ $E = (1 + \cos(2\alpha)) - (1 + \cos(2\alpha + 2\beta)) + \frac{3}{2}(1 + \cos(2\beta))$ $E = 1 + \cos(2\alpha) - 1 - \cos(2\alpha + 2\beta) + \frac{3}{2} + \frac{3}{2} \cos(2\beta)$ $E = \cos(2\alpha) - \cos(2\alpha + 2\beta) + \frac{3}{2} + \frac{3}{2} \cos(2\beta)$.

Let $A = 2\alpha$ and $B = 2\beta$. The expression becomes: $E = \frac{3}{2} + \cos A + \frac{3}{2} \cos B - \cos(A+B)$.

To find the maximum value, we can analyze this expression. Consider the case when $\beta = k\pi$ for some integer $k$. This implies $z = \tan(k\pi) = 0$. If $z=0$, the original equation becomes $x(0) + x + 0 = y$, so $y=x$. The expression $E$ becomes: $E = \frac{2}{1+x^2} - \frac{2}{1+x^2} + \frac{3}{1+0^2} = 0 + 3 = 3$. This value is attained for any real $x$ when $z=0$.

Let's verify this with the trigonometric form. If $\beta = k\pi$, then $B = 2\beta = 2k\pi$. $E = \frac{3}{2} + \cos A + \frac{3}{2} \cos(2k\pi) - \cos(A+2k\pi)$ $E = \frac{3}{2} + \cos A + \frac{3}{2}(1) - \cos A$ $E = \frac{3}{2} + \frac{3}{2} = 3$.

The greatest value of the expression is 3. We are given that the greatest value is $\frac{p}{q}$, where $p$ and $q$ are relatively prime. So, $\frac{p}{q} = 3 = \frac{3}{1}$. This means $p=3$ and $q=1$. They are relatively prime. We need to find the value of $(p-q)$. $p-q = 3 - 1 = 2$.