Question

Let x, y, z and t be real numbers such that (x, y) lies on a circle having radius 3, (z, t) lies on a circle having radius 4 and xt - yz = 12, then the greatest value of P = xz is ____ [Note: Both circles have centre at origi

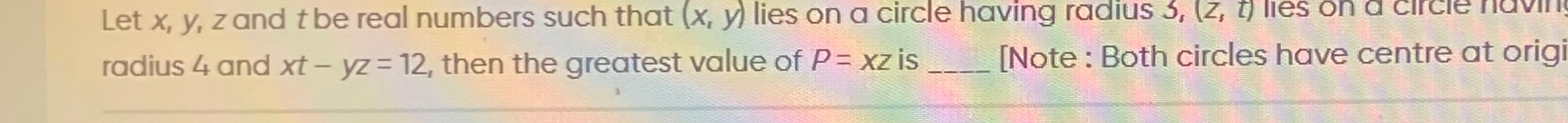
Answer 1

6

Answer 2

Solution:

Given that

$$x^2+y^2=9,\quad z^2+t^2=16,\quad xt-yz=12.$$

Step 1: Parameterize the points on the circles: Let

$$x=3\cos A,\quad y=3\sin A,\quad z=4\cos B,\quad t=4\sin B.$$

Step 2: Substitute in the condition $xt - yz = 12$:

$$(3\cos A)(4\sin B)-(3\sin A)(4\cos B)=12(\cos A\sin B-\sin A\cos B)=12.$$

Recall that $\cos A\sin B-\sin A\cos B=\sin(B-A)$. Thus,

$$12\sin(B-A)=12\quad \Rightarrow \quad \sin(B-A)=1.$$

The general solution is:

$$B-A=\frac{\pi}{2}+2k\pi,\quad k\in\mathbb{Z}.$$

Take $B=A+\frac{\pi}{2}$.

Step 3: Express $P=xz$ in terms of $A$:

$$P=xz=3\cos A\cdot 4\cos B=12\cos A \cos\left(A+\frac{\pi}{2}\right).$$

Using the identity $\cos\left(A+\frac{\pi}{2}\right)=-\sin A$:

$$P=12\cos A(-\sin A)=-12\cos A\sin A.$$

Utilize the double-angle identity:

$$\sin(2A)=2\sin A\cos A \quad \Rightarrow \quad \cos A\sin A=\frac{\sin(2A)}{2}.$$

So,

$$P=-12\cdot\frac{\sin(2A)}{2}=-6\sin(2A).$$

Step 4: Find the maximum value of $P$. Since $\sin(2A)$ varies between $-1$ and $1$, the maximum of $P=-6\sin(2A)$ occurs when $\sin(2A)$ is minimum:

$$\sin(2A)=-1\quad \Rightarrow \quad P_{\max}=-6(-1)=6.$$