Question
Question: Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function $f(x...
Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x)=∣[x]∣−3∣[x]∣−2 is (−∞,a)∪[b,c)∪[4,∞),a<b<c, then the value of a + b + c is :
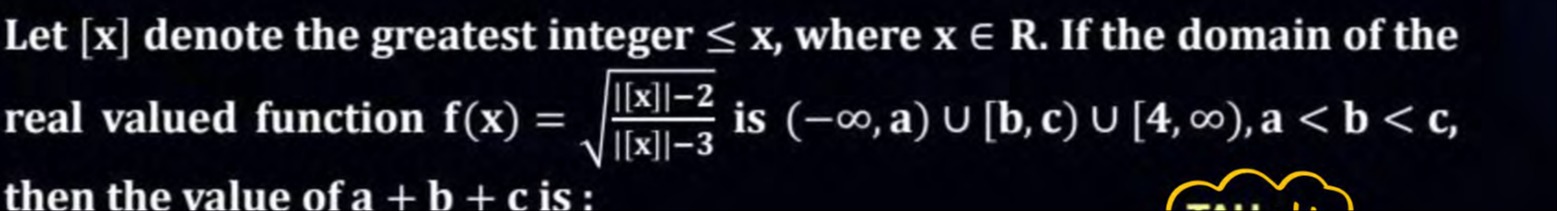
a = -3, b = -2, c = 3
a = -4, b = -2, c = 3
a = -3, b = -1, c = 3
a = -3, b = -2, c = 4
a = -3, b = -2, c = 3
Solution
The function given is f(x)=∣[x]∣−3∣[x]∣−2. For the function to be defined, two conditions must be met:
- The expression inside the square root must be non-negative: ∣[x]∣−3∣[x]∣−2≥0
- The denominator must not be zero: ∣[x]∣−3=0⟹∣[x]∣=3
Let y=∣[x]∣. Since [x] is an integer, y must be a non-negative integer. The inequality becomes: y−3y−2≥0 This inequality holds if both the numerator and denominator are positive, or both are negative.
Case 1: y−2≥0 and y−3>0 y≥2 and y>3. This implies y>3.
Case 2: y−2≤0 and y−3<0 y≤2 and y<3. This implies y≤2.
So, the condition on y is y≤2 or y>3. Substituting back y=∣[x]∣, we get: ∣[x]∣≤2or∣[x]∣>3
Let's solve these conditions for [x]:
Condition 1: ∣[x]∣≤2 This means −2≤[x]≤2. Since [x] must be an integer, the possible values for [x] are -2, -1, 0, 1, 2.
- If [x]=−2, then −2≤x<−1.
- If [x]=−1, then −1≤x<0.
- If [x]=0, then 0≤x<1.
- If [x]=1, then 1≤x<2.
- If [x]=2, then 2≤x<3. The union of these intervals is [−2,3).
Condition 2: ∣[x]∣>3 This means [x]>3 or [x]<−3.
- If [x]>3: Since [x] is an integer, this means [x]≥4. If [x]=4, then 4≤x<5. If [x]=5, then 5≤x<6, and so on. This corresponds to the interval [4,∞).
- If [x]<−3: Since [x] is an integer, this means [x]≤−4. If [x]=−4, then −4≤x<−3. If [x]=−5, then −5≤x<−4, and so on. This corresponds to the interval (−∞,−3).
Combining the results from both conditions, the domain of f(x) is the union of these intervals: Domain = (−∞,−3)∪[−2,3)∪[4,∞).
The problem states that the domain is (−∞,a)∪[b,c)∪[4,∞), with a<b<c. Comparing our derived domain with the given format:
- (−∞,a) corresponds to (−∞,−3), so a=−3.
- [b,c) corresponds to [−2,3), so b=−2 and c=3.
- [4,∞) matches the given interval.
We check the condition a<b<c: −3<−2<3. This condition is satisfied.
The question asks for the value of a+b+c. a+b+c=(−3)+(−2)+3 a+b+c=−5+3 a+b+c=−2.
