Question

Let [x] denote the greatest integer less than or equal to x. Then the values of x ∈ R satisfying the equation $[e^x]^2 + [e^x + 1] - 3 = 0$ lies in the interval:

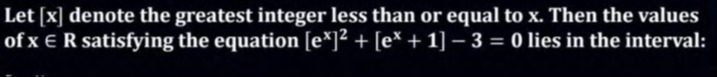
• A. [0, ln(2))
• B. (0, ln(2)]
• C. [-2, 1)
• D. (-2, 1]

Answer 1

Answer: (A)

[0, ln(2))

Answer 2

Let $k = [e^x]$. By the definition of the greatest integer function, $k$ must be an integer. The given equation is $[e^x]^2 + [e^x + 1] - 3 = 0$. Using the property $[y+n] = [y]+n$ for any integer $n$, we can rewrite $[e^x + 1]$ as $[e^x] + 1$. Substituting $k = [e^x]$ and $[e^x+1] = k+1$ into the equation, we get: $k^2 + (k+1) - 3 = 0$ Simplifying the equation: $k^2 + k - 2 = 0$ Factoring the quadratic equation: $(k+2)(k-1) = 0$ This yields two possible integer values for $k$: $k = -2$ or $k = 1$.

Case 1: $[e^x] = -2$ This inequality means that $-2 \le e^x < -1$. However, $e^x$ is always positive for all real values of $x$ ($e^x > 0$). Thus, $e^x$ cannot be less than $-1$. This case yields no real solutions for $x$.

Case 2: $[e^x] = 1$ This inequality means that $1 \le e^x < 2$. Taking the natural logarithm of all parts of the inequality: $\ln(1) \le \ln(e^x) < \ln(2)$ Using the properties $\ln(1) = 0$ and $\ln(e^x) = x$, we get: $0 \le x < \ln(2)$ This interval represents all the values of $x$ that satisfy the original equation.