Question

Let $\vec{a} = x\hat{i} + y\hat{j} + z\hat{k}$ makes equal angles with $\vec{b} = y\hat{i} - 2z\hat{j} + 3x\hat{k}$ and $\vec{c} = 2z\hat{i} + 3x\hat{j} - y\hat{k}$. Let $\vec{d} = \hat{i} - \hat{j} + 2\hat{k}$ such that $\vec{a} \perp \vec{d}$ and if $|\vec{a}| = 2\sqrt{3}$, then

The value of $\vec{a} \cdot \vec{b}$ is equal to

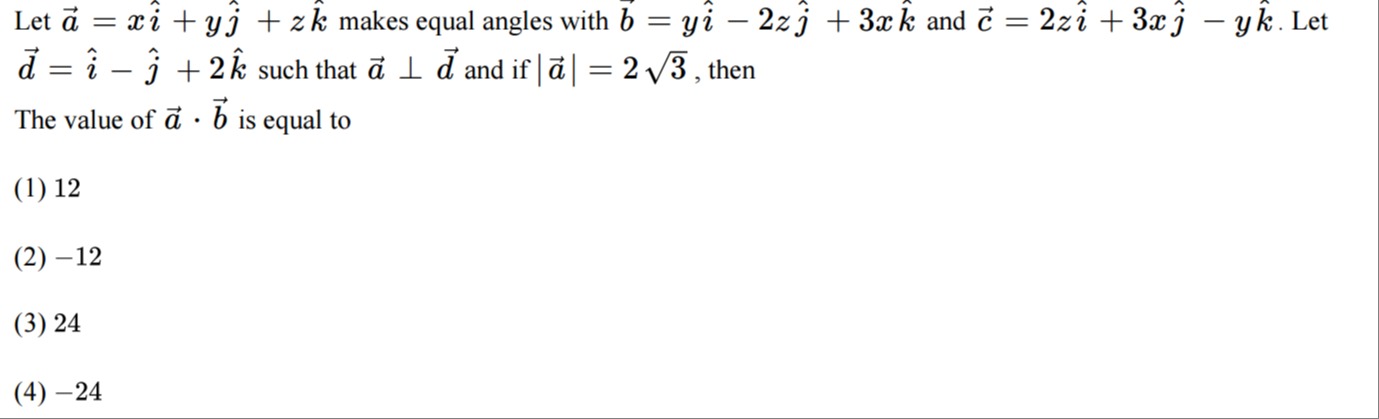
• A. 12
• B. -12
• C. 24
• D. -24

Answer 1

Answer: (D)

-24

Answer 2

Solution:

We are given:

$$\vec{a}=(x,y,z),\quad \vec{b}=(y,-2z,3x),\quad \vec{c}=(2z,3x,-y),$$

with $|\vec{a}|=2\sqrt{3}$ and $\vec{a}$ making equal angles with $\vec{b}$ and $\vec{c}$. Also, $\vec{a}\perp \vec{d}$, where $\vec{d}=(1,-1,2)$.

1. Equal Angle Condition:

Since $\vec{a}$ makes equal angles with $\vec{b}$ and $\vec{c}$ and $|\vec{b}|=|\vec{c}|$ (their components are just permuted),

$$\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\frac{\vec{a}\cdot \vec{c}}{|\vec{a}||\vec{c}|} \quad\Rightarrow\quad \vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}.$$

Calculate:

$$\vec{a}\cdot\vec{b}=xy-2yz+3xz,\qquad \vec{a}\cdot\vec{c}=2xz+3xy-yz.$$

Equate:

$$xy-2yz+3xz=2xz+3xy-yz.$$

Rearranging,

$$-2xy+xz-yz=0 \quad\Rightarrow\quad xz-yz=2xy.$$

Factor LHS:

$$z(x-y)=2xy. \quad \text{(i)}$$

2. Perpendicularity Condition:

$$\vec{a}\cdot\vec{d}=x-y+2z=0 \quad\Rightarrow\quad x-y=-2z. \quad \text{(ii)}$$

Substitute (ii) in (i):

$$z(-2z)=2xy\quad\Rightarrow\quad -2z^2=2xy \quad\Rightarrow\quad xy=-z^2. \quad \text{(iii)}$$

3. Find $x,y,z$:

Use (ii) to set $x-y=-2z$ and notice that if we choose $x+y=0$ then:

• Solve: $x+y=0$ and $x-y=-2z$ ⇒ Adding, $2x=-2z$ so $x=-z$ and hence $y=z$.
• Check (iii): $xy=(-z)(z)=-z^2$ holds.

Now, using $|\vec{a}|^2=x^2+y^2+z^2=12$:

$$(-z)^2+z^2+z^2=3z^2=12 \quad\Rightarrow\quad z^2=4.$$

Take $z=2$ (any choice works as the dot product is unique up to sign):

$$x=-2,\quad y=2,\quad z=2.$$

4. Compute $\vec{a}\cdot \vec{b}$:

$$\vec{a}\cdot \vec{b}=xy-2yz+3xz.$$

Substitute:

$$(-2)(2)-2(2)(2)+3(-2)(2)=-4-8-12=-24.$$

Thus, the answer is -24.