Question

Let $\vec{a} = \hat{i} + \hat{j} + \hat{k}$ and let $\vec{r}$ be a variable vector such that $\vec{r}.\hat{i}$, $\vec{r}.\hat{j}$ and $\vec{r}.\hat{k}$ are positive integers.

If $\vec{r}.\vec{a} \le 12$, then the total number of such vectors is:

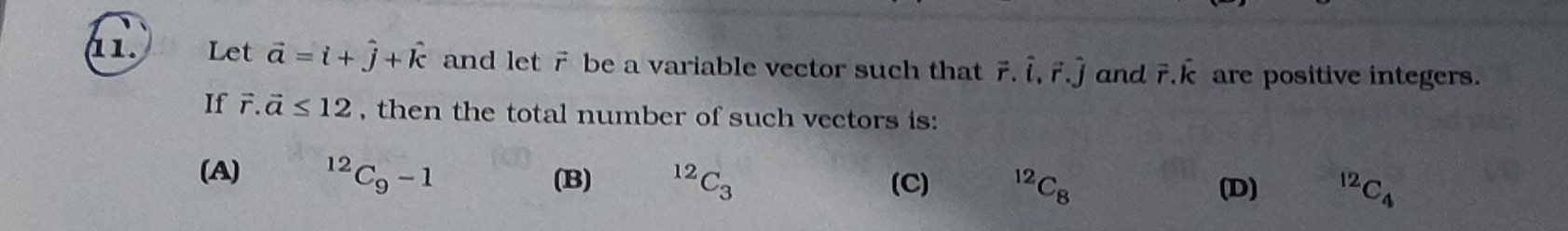
• A. $^{12}C_9 - 1$
• B. $^{12}C_3$
• C. $^{12}C_8$
• D. $^{12}C_4$

Answer 1

Answer: (B)

(B)

Answer 2

Let $\vec{r} = x\hat{i} + y\hat{j} + z\hat{k}$.

Given conditions:

1. $\vec{r}.\hat{i} = x$, $\vec{r}.\hat{j} = y$, $\vec{r}.\hat{k} = z$ are positive integers. So $x, y, z \ge 1$.
2. $\vec{a} = \hat{i} + \hat{j} + \hat{k}$.
3. $\vec{r}.\vec{a} \le 12$. This implies $x+y+z \le 12$.

We need to find the number of positive integer solutions $(x, y, z)$ for $x+y+z \le 12$.

Let $x' = x-1$, $y' = y-1$, $z' = z-1$. Then $x', y', z' \ge 0$.

Substituting these into the inequality:

$(x'+1) + (y'+1) + (z'+1) \le 12$

$x' + y' + z' + 3 \le 12$

$x' + y' + z' \le 9$.

To find the number of non-negative integer solutions for $x' + y' + z' \le 9$, we introduce a non-negative integer slack variable $s \ge 0$.

The inequality becomes an equation: $x' + y' + z' + s = 9$.

This is a stars and bars problem with $N=9$ (stars) and $k=4$ (variables $x', y', z', s$).

The number of solutions is given by $\binom{N+k-1}{k-1}$ or $\binom{N+k-1}{N}$.

Number of solutions = $\binom{9+4-1}{4-1} = \binom{12}{3}$.

Alternatively, Number of solutions = $\binom{9+4-1}{9} = \binom{12}{9}$.

Both expressions are numerically equal.

The total number of such vectors is $^{12}C_3$.