Question

Let $\vec{a},\vec{b}\text{ and }\vec{c}$ three unit vectors, out of which vectors $\vec{b}\text{ and }\vec{c}$ are non-parallel. If $\alpha$ and $\beta$ are the angles which vector $\vec{a}$ makes with vector $\vec{b}\text{ and }\vec{c}$ respectively and $\vec{a}\times \left( \vec{b}\times \vec{c} \right)=\dfrac{1}{2}\vec{b}$ then $\left| \alpha -\beta \right|$ is equal to:

& A{{.60}^{\circ }} \\\ & B{{.30}^{\circ }} \\\ & C{{.90}^{\circ }} \\\ & D{{.45}^{\circ }} \\\ \end{aligned}$$

Answer 1

To solve this question, we will use the formula of vector triple product of three vectors which is given as $\vec{p}\times \left( \vec{q}\times \vec{r} \right)=\left( \vec{p}\cdot \vec{r} \right)\vec{q}-\left( \vec{p}\cdot \vec{q} \right)\vec{r}$ where $\vec{p},\vec{q}\text{ and }\vec{r}$ are there vectors. Then, we will compare the value obtained to $\dfrac{1}{2}\vec{b}$ as we are given $\vec{a}\times \left( \vec{b}\times \vec{c} \right)=\dfrac{1}{2}\vec{b}$ then we will use the formula of dot product of two vector when angle between them is given, $\vec{p}\cdot \vec{q}=\left| {\vec{p}} \right|\left| {\vec{q}} \right|\cos \theta$ where $\vec{p}\text{ and }\vec{q}$ are two vectors and $\theta$ is the angle between them.

Complete step by step answer:
Given that $\vec{a},\vec{b}\text{ and }\vec{c}$ are unit vectors.
Let us first define a unit vector. A unit vector is a vector having magnitude as 1. That is, if $\vec{p}$ is a unit vector than $\left| {\vec{p}} \right|=1$
If $\vec{p}=x\hat{i}+y\hat{i}+z\hat{k}$ then magnitude of $\vec{p}=\left| {\vec{p}} \right|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$
As $\vec{a},\vec{b}\text{ and }\vec{c}$ are unit vector $\left| {\vec{a}} \right|=1,\left| {\vec{b}} \right|=1\text{ and }\left| {\vec{c}} \right|=1$
Given that $\alpha$ is angle between vector $\vec{d}\text{ and }\vec{b}$

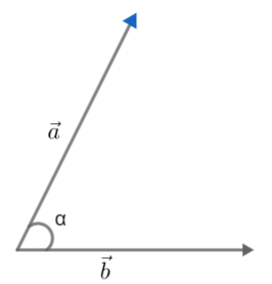
And $\beta$ is angle between $\vec{a}\text{ and }\vec{c}$

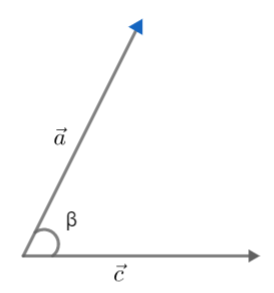
Now, we will define a vector triple product.
Vector triple product of three vectors $\vec{p},\vec{q}\text{ and }\vec{r}$ is defined as the cross product of the $\vec{p}$ with cross product of $\vec{q}\text{ and }\vec{r}$
It is represented as $\vec{p}\times \left( \vec{q}\times \vec{r} \right)$
The formula for vector triple product is

& \vec{p}\times \left( \vec{q}\times \vec{r} \right)=\left( \vec{p}\cdot \vec{r} \right)\vec{q}-\left( \vec{p}\cdot \vec{q} \right)\vec{r} \\\ & \Rightarrow \vec{p}\times \left( \vec{q}\times \vec{r} \right)=\left( \vec{p}\cdot \vec{r} \right)\vec{q}-\left( \vec{q}\cdot \vec{r} \right)\vec{p} \\\ \end{aligned}$$ In general we have $$\vec{p}\times \left( \vec{q}\times \vec{r} \right)\ne \left( \vec{p}\times \vec{q} \right)\times \vec{r}$$ We are given that $$\vec{a}\times \left( \vec{b}\times \vec{c} \right)=\dfrac{1}{2}\vec{b}$$ which is vector triple product of $\vec{a},\vec{b}\text{ and }\vec{c}$ Using the formula of vector triple product we have: $$\vec{a}\times \left( \vec{b}\times \vec{c} \right)=\left( \vec{a}\cdot \vec{c} \right)\vec{b}-\left( \vec{a}\cdot \vec{b} \right)\vec{c}$$ We had $$\begin{aligned} & \vec{a}\times \left( \vec{b}\times \vec{c} \right)=\dfrac{1}{2}\vec{b} \\\ & \left( \vec{a}\cdot \vec{c} \right)\vec{b}-\left( \vec{a}\cdot \vec{b} \right)\vec{c}=\dfrac{1}{2}\vec{b}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)} \\\ \end{aligned}$$ Comparing both sides of above equation and coefficient of vector $\vec{b}$ we get that $$\left( \vec{a}\cdot \vec{c} \right)\vec{b}=\dfrac{1}{2}\vec{b}\text{ and }-\left( \vec{a}\cdot \vec{b} \right)\vec{c}=0\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}$$ This is so as there is no term on RHS of (i) having $\vec{c}$ Again comparing terms of $$\left( \vec{a}\cdot \vec{c} \right)\vec{b}=\dfrac{1}{2}\vec{b}$$ and cancelling vector $\vec{b}$ we get $$\left( \vec{a}\cdot \vec{c} \right)=\dfrac{1}{2}$$ We have a formula of dot product of two vectors $\vec{p}\text{ and }\vec{q}$ when angle between them is $\theta $ is given as $$\vec{p}\cdot \vec{q}=\left| {\vec{p}} \right|\left| {\vec{q}} \right|\cos \theta $$ Where $\vec{p}$ is magnitude of $\vec{p}\text{ and }\left| {\vec{q}} \right|$ is magnitude of $\vec{q}$ Using this formula above in $\vec{a}\cdot \vec{c}=\dfrac{1}{2}$ we get $$\left| {\vec{a}} \right|\left| {\vec{c}} \right|\cos \beta =\dfrac{1}{2}$$ This is so as we had angle between $\vec{a}\text{ and }\vec{c}$ as $\beta $ Now, $\vec{a}\text{ and }\vec{c}$ are both unit vectors $\left| {\vec{a}} \right|=1\text{ and }\left| {\vec{c}} \right|=1$ Substituting this in above equation we get: $$\begin{aligned} & 1\cdot 1\cos \beta =\dfrac{1}{2} \\\ & \cos \beta =\dfrac{1}{2} \\\ \end{aligned}$$ Now, we know that value of $$\cos \dfrac{\pi }{3}=\dfrac{1}{2}\Rightarrow \cos \beta =\cos \dfrac{\pi }{3}$$ Applying $${{\cos }^{-1}}$$ both sides we get: $$\beta =\dfrac{\pi }{3}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iii)}$$ We have obtained from equation (ii) that $$\begin{aligned} & 0=-\left( \vec{a}\cdot \vec{b} \right)\cdot \vec{c} \\\ & \left( \vec{a}\cdot \vec{b} \right)\cdot \vec{c}=0 \\\ \end{aligned}$$ Now, as $\vec{c}$ is unit vector $\left| {\vec{c}} \right|=1$ then $$\begin{aligned} & \left( \vec{a}\cdot \vec{b} \right)\cdot \vec{c}=0 \\\ & \vec{a}\cdot \vec{b}=0 \\\ \end{aligned}$$ Now, applying formula of dot product stated above between $\vec{a}\text{ and }\vec{b}$ we get: $$\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \alpha =0$$ As angle between $\vec{a}\text{ and }\vec{b}$ is $\alpha $ Now, as $\left| {\vec{a}} \right|=1=\left| {\vec{b}} \right|$ as both $\vec{a}\text{ and }\vec{b}$ are unit vector. $$\begin{aligned} & 1\cdot 1\cdot \cos \alpha =0 \\\ & \cos \alpha =0 \\\ \end{aligned}$$ We know that $$\cos \dfrac{\pi }{2}=0\Rightarrow \cos \alpha =\cos \dfrac{\pi }{2}$$ Applying ${{\cos }^{-1}}$ both sides of above equation we get $$\alpha =\dfrac{\pi }{2}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iv)}$$ So from equation (iii) and (iv) we have $\alpha =\dfrac{\pi }{2}\text{ and }\beta =\dfrac{\pi }{3}$ Then value of $$\begin{aligned} & \left| \alpha -\beta \right|=\left| \dfrac{\pi }{2}-\dfrac{\pi }{3} \right| \\\ & \left| \alpha -\beta \right|=\left| \dfrac{3\pi -2\pi }{6} \right|=\left| \dfrac{\pi }{6} \right| \\\ \end{aligned}$$ Value of $\left| \alpha -\beta \right|=\left| \dfrac{\pi }{6} \right|\Rightarrow {{30}^{\circ }}$ **So, the correct answer is “Option B”.** **Note:** The possibility of confusion in this question can be at the point where we have used $$\left( \vec{a}\cdot \vec{b} \right)\cdot \vec{c}=0\Rightarrow \vec{a}\cdot \vec{b}=0$$ this is possible as $\vec{c}$ is a unit vector. $\vec{c}$ being unit vector $\left| {\vec{c}} \right|=1$ hence if the magnitude of any vector is 1 or non-zero then it cannot be a 0 vector. So, only possibility left is that $$\vec{a}\cdot \vec{b}=0$$