Question

Let $V$ be the potential and $E$ be the magnitude of the electric field. At a given position, which one of the following statement is true:
A. $E$ is always zero where $V$ is zero.
B. $V$ is always zero where $E$ is zero.
C. $E$ can be zero where $V$ is non-zero.
D. $E$ is always non-zero where $V$ is non-zero.

Answer 1

Electric potential at a point is the work done to bring a unit positive charge from infinity to that point. Whereas, the electric field is the region around which the effect of a charge can be felt. It tells us about the force experienced by a test charge at a particular point with respect to that charge.

Formula used:
Electric Field, $E = \dfrac{{kq}}{{{r^2}}}$
Where: $E = Electric{\text{ field intensity at a point}}$
$\Rightarrow k = 9 \times {10^9}kg{m^3}{s^ - }^2{C^ - }^2 \\\ \Rightarrow q = ch\arg e \\\ \Rightarrow r = dis\tan ce{\text{ between two charges}} \\\$
Electric potential, $V = \dfrac{{k{q_{}}}}{r}$
Where:$V = potential$
$\Rightarrow k = 9 \times {10^9}kg{m^3}{s^ - }^2{C^ - }^2 \\\ \Rightarrow q = ch\arg e \\\ \Rightarrow r = dis\tan ce{\text{ between two charges}} \\\$
The relation between electric field and potential is given as:
$E = - \dfrac{{dv}}{{dr}}$

Complete step by step answer:
Let us consider a case where two charges of opposite polarity and same magnitude are kept at a distance of $2d$ from each other.

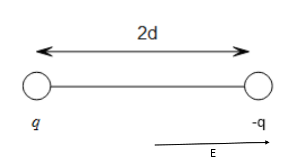
Here we see that the potential due to the charges is zero at the center as they are of opposite polarity but there is a net electric field towards the right. So, it concludes that even though the potential at a point is zero the electric field need not be zero at that point.

Now, in the next case assume two charges of same magnitude and polarity are kept at a distance $2d$ from each other.

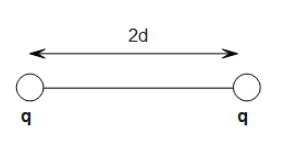
Here both the charges are of equal magnitude so the electric potential at the center will not be zero in this case but electric field will be zero. Therefore we can conclude that electric field (E) can be non-zero even if potential (V) at a point is zero.

So, option C is the correct answer.

Note: Potential at any point is always measured with respect to another point. There is no such thing as absolute potential. In general potential at an infinite distance is taken as zero. Potential is a scalar quantity which means that it only has magnitude but no direction.Whereas, the electric field is a vector quantity as it has both magnitude and direction.