Question

Let us denote the point $P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ on the parabola ${{y}^{2}}=4ax$ on the parabola as $P\left( {{t}_{1}} \right)$. Tangents are drawn from the points $P\left( {{t}_{1}} \right),Q\left( {{t}_{2}} \right),R\left( {{t}_{3}} \right)$ to the parabola. Prove that the orthocenter of the triangle formed by the tangents and the point $S\left( 0,a{{t}_{1}}{{t}_{2}}{{t}_{3}}+a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right) \right)$ are equidistant from the axis of the parabola.

Answer 1

Hint: Use the parametric form of the equation of a tangent to a parabola. Use the fact that tangents drawn to a parabola at ${{t}_{1}}$ and ${{t}_{2}}$ intersect at $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$ and the slope of the tangent drawn at $P\left( t \right)$ has the slope as $\dfrac{1}{t}$. Hence find the coordinates of the orthocenter of the triangle formed. Hence prove that the orthocentre and the point are equidistant from the axis of the parabola.

Complete step-by-step answer:

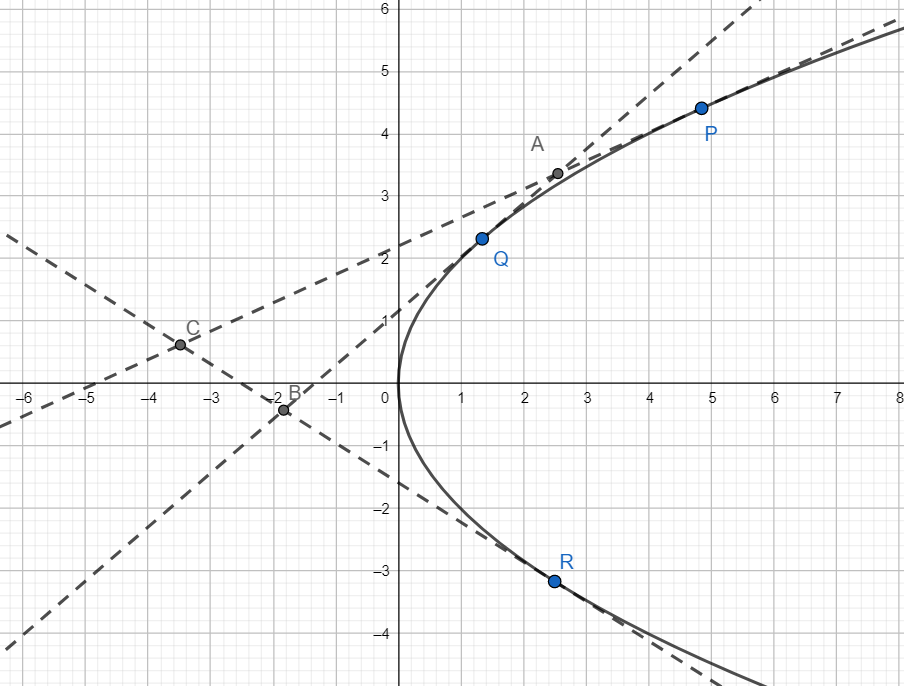
We have the equation of the tangent at $P\left( {{t}_{1}} \right)$ is given by
$y{{t}_{2}}=x+a{{t}_{1}}^{2}\text{ (i)}$
Similarly, the equation of the tangent at $Q\left( {{t}_{2}} \right)$ is given by
$y{{t}_{2}}=x+a{{t}_{2}}^{2}\text{ (ii)}$
And the equation of the tangent at $R\left( {{t}_{3}} \right)$ is given by
$y{{t}_{3}}=x+a{{t}_{3}}^{2}\text{ (iii)}$
We know that the tangents at $P\left( {{t}_{1}} \right)$ and $Q\left( {{t}_{2}} \right)$ intersect at the point $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$
Hence we have $A\equiv \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$ and $B\equiv \left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)$
Since the slope of the tangent at R is $\dfrac{1}{{{t}_{3}}}$, we have
The slope of altitude from point A is $\dfrac{-1}{\dfrac{1}{{{t}_{3}}}}=-{{t}_{3}}$
Hence, the equation of altitude from A is given by
$\begin{aligned} & y-a\left( {{t}_{1}}+{{t}_{2}} \right)=-{{t}_{3}}\left( x-a{{t}_{1}}{{t}_{2}} \right) \\\ & \Rightarrow y-x{{t}_{3}}=a{{t}_{1}}{{t}_{2}}{{t}_{3}}+a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right)-a{{t}_{3}} \\\ & \Rightarrow y-x{{t}_{3}}+a{{t}_{3}}=C\text{ (iv)} \\\ \end{aligned}$
where $C=a{{t}_{1}}{{t}_{2}}{{t}_{3}}+a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right)$
Similarly, the equation of the tangent through B is given by
$y-x{{t}_{1}}+a{{t}_{1}}=C\text{ (v)}$
Multiplying equation (iv) by ${{t}_{1}}$ and equation (v) by ${{t}_{3}}$ and subtracting equation (iv) from equation (v), we get
${{t}_{3}}y-{{t}_{1}}y-x{{t}_{3}}{{t}_{1}}+x{{t}_{3}}{{t}_{1}}+a{{t}_{3}}{{t}_{1}}-a{{t}_{3}}{{t}_{1}}=C{{t}_{3}}-C{{t}_{1}}$
Hence, we have
$y\left( {{t}_{3}}-{{t}_{1}} \right)=C\left( {{t}_{3}}-{{t}_{1}} \right)$
Hence, we have $y=a{{t}_{1}}{{t}_{2}}{{t}_{3}}+a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right)$
Hence the distance of orthocentre from the axis of the parabola is $a{{t}_{1}}{{t}_{2}}{{t}_{3}}+a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right)$ which is the same as the distance of S from the x-axis.

Note: In these types of questions we need to remember the equations of tangents in parametric form and also the coordinates of the point of intersection of tangents at two points on the parabola. The coordinates of the point of intersection of tangents at points $P\left( {{t}_{1}} \right)$ and $Q\left( {{t}_{2}} \right)$ can be remembered as follows:
G O A rule:
G stands for the geometric mean of the x -coordinates:
A stands for the arithmetic mean of the y-coordinates.
$G={{\left( a{{t}_{1}}^{2}a{{t}_{2}}^{2} \right)}^{\dfrac{1}{2}}}=a{{t}_{1}}{{t}_{2}}$ and $A=\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2}=a\left( {{t}_{1}}+{{t}_{2}} \right)$
Hence the coordinates of the point of intersection are $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$