Question

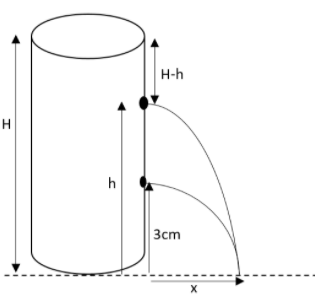
Let us assume that two holes are created in the side of the tank such that the jets of water flowing out of them meet at the identical position on the ground. When one hole is at a height of $3cm$ above the bottom, then what will be the distance of the other holes from the top surface of water?

Answer 1

The velocity of efflux can be found by taking the square root of twice the product of acceleration due to gravity and height from the free surface. The time of flight can be found by taking the square root of the ratio of twice the height of hole to the acceleration due to gravity.

Complete answer:
The velocity of efflux can be found by taking the square root of twice the product of acceleration due to gravity and height from the free surface.

That is we can write that,
$V=\sqrt{2gh}$
Where $h$ be the distance from the free surface.
Let us check the figure first. For the first hole, let us assume that the velocity of efflux be ${{V}_{1}}$, $g$ be the acceleration of the gravity. Therefore we can write that,
${{V}_{1}}=\sqrt{2g\left( H-3 \right)}$
The time of flight of the first hole can be found by the equation,
${{t}_{1}}=\sqrt{\dfrac{2\times 3}{g}}$
The range of the flow can be found by taking the product of the velocity of efflux and the time of flight. This can be written as,
$x={{V}_{1}}\times {{t}_{1}}$
Substituting the values in it,
$\begin{aligned} & x=\sqrt{2g\left( H-3 \right)\times \sqrt{\dfrac{2\times 3}{g}}} \\\ & \Rightarrow x=\sqrt{12\left( H-3 \right)} \\\ \end{aligned}$
For the second hole, the velocity of efflux can be shown as ${{V}_{2}}$.
This can be found as,
${{V}_{2}}=\sqrt{2g\left( H-h \right)}$
And the time of flight can be found as,
${{t}_{2}}=\sqrt{\dfrac{2h}{g}}$
The range of the flow can be found by the equation,
$x={{V}_{2}}\times {{t}_{2}}$
Substituting the values in this will give,
$x=\sqrt{4h\left( H-h \right)}$
As the water flowing out of them meet at the identical position on the ground, their range of flow will be similar. That is,
$\sqrt{4h\left( H-h \right)}=\sqrt{12\left( H-3 \right)}$
Simplifying this equation can be written as,

& 4h\left( H-h \right)=12\left( H-3 \right) \\\ & \Rightarrow h\left( H-h \right)=3\left( H-3 \right) \\\ \end{aligned}$$ ………… (2) Now let us redraw the diagram.  Here the distance of the second hole from the top surface will be given as $${{h}_{1}}$$. Therefore the horizontal range of the first hole can be written as the same itself. That is, $$x=\sqrt{12\left( H-3 \right)}$$……. (1) The velocity of efflux from the second hole can be written as, $${{V}_{2}}^{\prime }=\sqrt{2g{{h}_{1}}}$$ The time of flight of the second hole can be shown as, $${{t}_{2}}^{\prime }=\sqrt{\dfrac{2\left( H-{{h}_{1}} \right)}{g}}$$ Therefore the horizontal range will become, $$x={{V}_{2}}^{\prime }\times {{t}_{2}}^{\prime }$$ Substituting the values in it will give, $$x=\sqrt{4{{h}_{1}}\left( H-{{h}_{1}} \right)}$$ This can be compared with the equation (1) as, $$4{{h}_{1}}\left( H-{{h}_{1}} \right)=12\left( H-3 \right)$$ That is, $${{h}_{1}}\left( H-{{h}_{1}} \right)=3\left( H-3 \right)$$……… (3) Compare equation (3) with the equation (2) as, $${{h}_{1}}\left( H-{{h}_{1}} \right)=h\left( H-h \right)$$ From this equation, we can write that, $${{h}_{1}}=h$$ This result shows that in order to make these distances equal, the distance from the top surface should be equal to the distance from the ground. Therefore the distance from the top surface will be obtained as $${{h}_{1}}=3cm$$. **Note:** The horizontal range of a projectile is defined as the distance along the horizontal plane a body can travel, before reaching the similar vertical position like it started from. The horizontal range is dependent on the initial velocity, the launch angle and the acceleration due to gravity.