Question

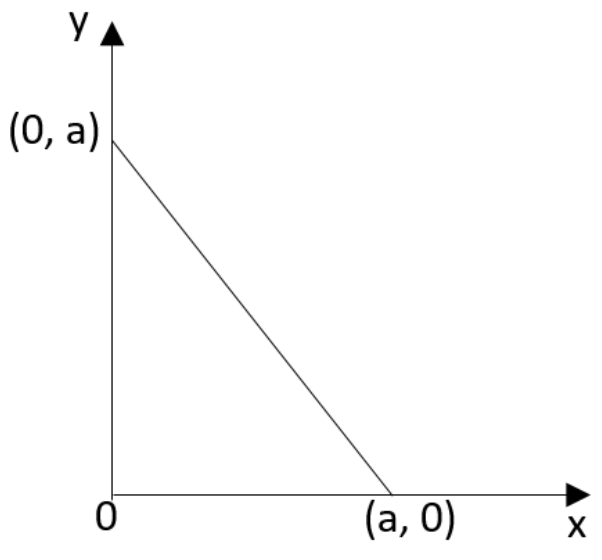
let us assume that three rods of identical mass are placed as represented in the diagram. What can be the coordinate of the center of mass of the system?

$\begin{aligned} & A.\left( \dfrac{a}{2},\dfrac{a}{2} \right) \\\ & B.\left( \dfrac{a}{\sqrt{2}},\dfrac{a}{\sqrt{2}} \right) \\\ & C.\left( \dfrac{a}{3},\dfrac{a}{3} \right) \\\ & D.\left( \dfrac{a}{\sqrt{3}},\dfrac{a}{\sqrt{3}} \right) \\\ \end{aligned}$

Answer 1

In the case of a uniform rod its center of mass will be the exact midpoint of this rod. First of all, find out the center of mass of each rod. Using this find the center of the system. The center of mass of the body can be found by taking the ratio of the product of the mass of the rod and the sum of the individual position of the three rods to the sum of the masses of the three rods. This will help you in answering this question.

Complete step by step solution:
In the case of a uniform rod its centre of mass will be the exact midpoint of this rod. Therefore the centre of mass of the vertical rod can be found to be as$\left( 0,\dfrac{a}{2} \right)$. The centre of mass of the horizontal rod can be found to be as$\left( \dfrac{a}{2},0 \right)$. And the centre of mass of the inclined rod can be found to be as $\left( \dfrac{a}{2},\dfrac{a}{2} \right)$.
The center of mass of the body can be found by taking the ratio of the product of the mass of the rod and the sum of the individual position of the three rods to the sum of the masses of the three rods. Therefore the x coordinate of the centre of mass can be written as,
$x=\dfrac{m\left( 0+0.5a+0.5a \right)}{m+m+m}$
This has been obtained from the figure mentioned in the question.
Simplifying this equation can be written as,
$x=\dfrac{a}{3}$
The y coordinate of the centre of mass can also be found in the similar way. That is,
$y=\dfrac{m\left( 0.5a+0+0.5a \right)}{m+m+m}$
This can be simplified as,
$y=\dfrac{a}{3}$
Therefore the coordinates of the centre of mass will be found to be as $\left( \dfrac{a}{3},\dfrac{a}{3} \right)$. This has been mentioned as option C.

Note: The center of mass of the body can be defined as the imaginary point where the whole mass of the system is to be concentrated. This point will be having each and every property of the material. The center of mass can be found to be located either inside the material or outside the material.