Question

Let us assume that one mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as represented in the diagram. What will be the variation in internal energy of the gas at the time of transition?

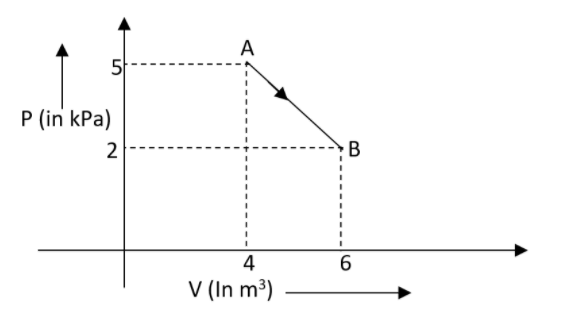
$\begin{aligned} & A.20J \\\ & B.-12kJ \\\ & C.20kJ \\\ & D.-20kJ \\\ \end{aligned}$

Answer 1

The change in internal energy can be found by taking the product of the number of moles of the gas, the specific heat capacity at constant volume and the change in temperature. Find the temperature for each condition using the ideal gas equation. Substitute this in the change in internal energy equation. This will help us to solve this question.

Complete step by step answer:
The change in internal energy can be found by taking the product of the number of moles of the gas, the specific heat capacity at constant volume and the change in temperature.
That is we can write that,
$\Delta U=n{{C}_{V}}\Delta T$
Where $n$ be the number of moles, ${{C}_{V}}$ be the specific heat capacity at constant volume and $\Delta T$ be the change in temperature.
For an ideal diatomic gas, the specific heat capacity at constant volume will be,
${{C}_{V}}=\dfrac{3}{2}R$
From the ideal gas equation we can write that,
$T=\dfrac{PV}{R}$
Where $P$ be the pressure, $V$ be the volume and $R$ be universal gas constant.
This can be applied in both the conditions such as,

& {{T}_{1}}=\dfrac{{{P}_{1}}{{V}_{1}}}{R} \\\ & {{T}_{2}}=\dfrac{{{P}_{2}}{{V}_{2}}}{R} \\\ \end{aligned}$$ Substituting these in the change in internal energy equation will give, $$\begin{aligned} & \Delta U={{C}_{V}}\left( {{T}_{2}}-{{T}_{1}} \right) \\\ & \Rightarrow \Delta U=\dfrac{3}{2}R\left( \dfrac{{{P}_{2}}{{V}_{2}}}{R}-\dfrac{{{P}_{1}}{{V}_{1}}}{R} \right) \\\ \end{aligned}$$ Cancelling the common terms in the equation can be written as,$$\Delta U=\dfrac{3}{2}\left( {{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}} \right)$$ Substituting the values in it, $$\begin{aligned} & \Delta U=\dfrac{3}{2}\left( 5\times 4-2\times 6 \right) \\\ & \Delta U=-12kJ \\\ \end{aligned}$$ **So, the correct answer is “Option B”.** **Note:** The internal energy of a thermodynamic system is defined as the energy included within it. It will be the energy required to produce or prepare the system in any certain internal state. The internal energy is found to be an extensive property, and this cannot be measured directly.