Question
Question: let us assume that a toy car of mass \(m\) is having two identical rubber ribbons connected to it as...
let us assume that a toy car of mass m is having two identical rubber ribbons connected to it as shown in the diagram. The force constant of each rubber ribbon will be given as K and the surface is frictionless. The car is made to displace from the mean position by xcm and released. At the mean position, the ribbons are undeformed. What will be the vibration period?
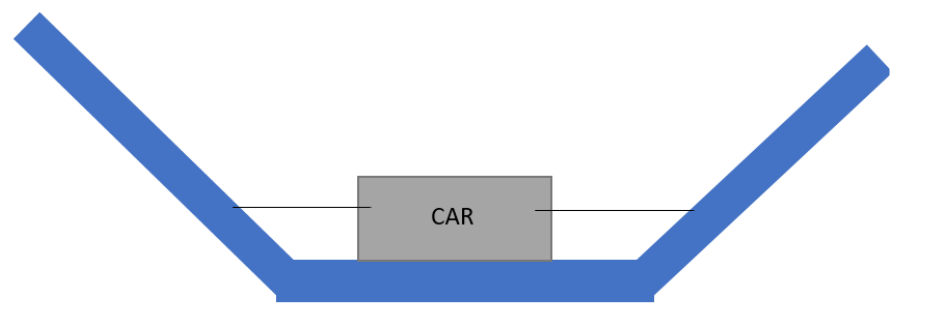
A.2πK2m(2K)B.2π1K2m(2K)C.2πKmD.2πK+Km
Solution
The force of the spring will be equivalent to the product of the spring constant and the distance traveled. From this find the acceleration of the system. The square of the angular velocity of the body will be found as the ratio of the spring constant to the mass of the body. Using this, find the time period. This can be helpful while answering this question.
Complete step-by-step solution
let us displace the car by a distance x, one of the rubber will get stretched by x but the other will lose to execute any force as rubber can’t be compressed like spring.
F=Kxma=Kx
Rearranging the equation can be written as,
a=mKx
The square of the angular velocity of the body will be found as the ratio of the spring constant to the mass of the body. That is we can write that,
ω2=mK
Substituting this value in the equation can be shown as,
a=ω2x
Where the angular velocity will be,
ω=mK
As we all know, the time period of oscillation or vibration will be the ratio of 2π to the angular velocity. This can be written as an equation given as,
T=ω2π
Substituting the values in it will give,
T=2πKm
Therefore the time period has been calculated. The answer has been mentioned as option C.
Note: The time period of a body is the time taken for a body in order to complete one single oscillation. The unit has been given as second. The frequency is the number of oscillations done in a unit period of time. This has been found by taking the reciprocal of the time period. Its unit is given as hertz.
